Lucru mecanic

Parte a seriei de articole despre
Mecanică clasică
${\displaystyle {\vec {F}}=m{\vec {a}}}$ Principiul al II-lea al mecanicii
Istorie Cronologie
Ramuri Cinematică Dinamică Mecanică cerească aplicată a mediilor continue statistică Statică
Concepte Accelerație Energie cinetică potențială Forță aparentă frecare Impuls Inerție Lucru mecanic virtual Masă Moment cinetic de inerție Principiul lui D'Alembert Putere Sistem de referință inerțial neinerțial Spațiu Timp Viteză relativă
Formulări Legile lui Newton Mecanică analitică Mecanică lagrangiană Mecanică hamiltoniană Ecuația Hamilton–Jacobi
Subiecte de bază Deplasare Legea atracției universale Mișcare ecuații armonică rectilinie Solid rigid
Rotație Rotație Sistem de referință în rotație Viteză unghiulară Accelerație unghiulară Forță centripetă centrifugă Forța Coriolis Frecvență Oscilație oscilator armonic amortizare Pendul conic Vibrație
Oameni de știință Galileo Huygens Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy
Categorii Mecanică clasică
v d m

Lucrul mecanic este o mărime fizică definită ca produsul dintre componenta forței care acționează asupra unui corp în direcția deplasării punctului ei de aplicație și mărimea drumului parcurs.^[1] E o mărime ce caracterizează schimbarea stării dinamice a sistemului. Lucrul mecanic este o mărime fizică derivată, scalară, extensivă în raport cu drumul, având caracter de mărime de transformare legată de variația mărimii de stare energie. Analitic, lucrul mecanic elementar efectuat pentru un drum infinitezimal ${\displaystyle \scriptstyle d{\vec {r}}}$ se definește ca produsul scalar al forței și deplasării (drumului infinitezimal): ${\displaystyle \scriptstyle \delta L={\vec {F}}\cdot d{\vec {r}}=F\,dr\cdot \cos \alpha }$. În general, lucrul mecanic nu admite diferențială totală exactă decât în anumite cazuri speciale cum ar fi mișcarea sub acțiunea forțelor conservative.

Terminologie

Termenul de lucru (în franceză travail) al unei forțe a fost utilizat pentru prima oară într-un articol din 1826 al matematicianului și inginerului mecanic francez Gaspard-Gustave Coriolis și apoi în cartea Du calcul de l'effet des machines din 1829 a aceluiași autor.^[2][3]

Înainte de denumirea dată de Coriolis, Carnot se referea la acest concept cu numele putere motrice în lucrarea sa din 1824 Despre puterea motrice a focului (Sur la puissance motrice du feu).

Denumirea de lucru mecanic a fost introdusă de Jean-Victor Poncelet.

Variația energiei unui sistem

Efectuarea unui lucru mecanic asupra unui (respectiv, de către un) sistem fizic duce la modificarea energiei sistemului cu o cantitate egală cu lucrul mecanic efectuat asupra sistemului (respectiv, de către sistem). Așadar, lucrul mecanic este o formă a schimbului de energie între un sistem și lumea înconjurătoare.^[4]

Teorema de variație a energiei într-un sistem neconservativ

În cazul în care într-un sistem apar forțe neconservative:^[5]

${\displaystyle L_{tot}=\Delta E_{c}}$

Unde L_tot este lucrul mecanic total, iar E_c este energia cinetică.

Lucrul mecanic al forțelor conservative este:^[5]

${\displaystyle L_{Fc}=-\Delta E_{p}}$

unde E_p este energia potențială.

Lucrul mecanic al forțelor neconservative este:^[5]

${\displaystyle L_{Fnc}=\Delta E_{mec}}$

unde unde E_mec este energia mecanică.

Definirea matematică generală

Pentru o forță constantă ${\displaystyle {\vec {F}}}$ care își deplasează punctul de aplicație după un segment de dreaptă ${\displaystyle {\vec {s}}}$, lucrul mecanic efectuat L este egal cu produsul scalar:

${\displaystyle L={\vec {F}}\cdot {\vec {s}}=F\,s\cdot \cos \alpha }$

${\displaystyle (3.1)}$

unde α este unghiul dintre direcția forței și direcția de deplasare. Lucrul mecanic este pozitiv dacă punctul de aplicație se deplasează în același sens cu forța (α<90°), negativ dacă punctul de aplicație se deplasează în sens invers forței (α>90°) și nul dacă punctul de aplicație este fix sau se deplasează perpendicular pe direcția forței (α=90°).

În cazul general, lucrul mecanic este definit ca o integrală curbilinie: ^[6]

${\displaystyle L=\int _{P1}^{P2}{\vec {F}}\mathrm {d} {\vec {s}}=\int _{P1}^{P2}F\mathrm {d} s\cos \alpha }$

${\displaystyle (3.2)}$

unde ${\displaystyle {\vec {s}}}$ este vectorul de poziție al punctului de aplicație al forței, iar P1 și P2 sunt pozițiile inițială și finală ale deplasării.

Folosind exprimarea analitică a vectorilor ${\displaystyle {\vec {F}}}$ și ${\displaystyle d{\vec {r}}\!}$ în funcție de proiecțiile vectorilor pe axele unui sistem cartezian Oxyz:

${\displaystyle {\vec {F}}={\vec {i}}F_{x}+{\vec {j}}F_{y}+{\vec {k}}F_{z};\;\;d{\vec {s}}={\vec {i}}dx+{\vec {j}}dy+{\vec {k}}dz}$

${\displaystyle (3.3)}$

expresia (3.2) devine:

${\displaystyle dL=F_{x}dx+F_{y}dy+F_{z}dz}$

${\displaystyle (3.4)}$

În funcție de viteza ${\displaystyle {\vec {v}}={\dot {\vec {s}}},\!}$ expresia lucrului mecanic elementar este:

${\displaystyle dL={\vec {F}}\cdot {\vec {v}}\cdot dt=(F_{x}{\dot {x}}+F_{y}{\dot {y}}+F_{z}{\dot {z}})dt.}$

${\displaystyle (3.5)}$

Proprietăți

a) este o mărime scalară având ca unitate de măsură în sistemul internațional SI joule-ul (J), iar în sistemul MKfS (sistemul tehnic de unități) kilogram-forță - metrul (kgf.m);

b) este pozitiv când ${\displaystyle \angle ({\vec {F}}\cdot d{\vec {r}})=\alpha \in (0,{\frac {\pi }{2}})\!}$ și poartă în acest caz numele de lucru mecanic motor

c) este negativ când ${\displaystyle \angle ({\vec {F}}\cdot d{\vec {r}})=\alpha \in ({\frac {\pi }{2}},\pi )\!}$ și poartă în acest caz numele de lucru mecanic rezistent

d) este nul când ${\displaystyle \alpha ={\frac {\pi }{2}}\!}$

e) dacă deplasarea ${\displaystyle d{\vec {r}}\!}$ este compusă din n deplasări elementare:

${\displaystyle d{\vec {r}}=d{\vec {r}}_{1}+d{\vec {r}}_{2}+\cdots d{\vec {r}}_{n}}$

${\displaystyle (4.1)}$

atunci:

${\displaystyle dL={\vec {F}}\cdot d{\vec {r}}={\vec {F}}\cdot d{\vec {r}}_{1}+{\vec {F}}\cdot d{\vec {r}}_{2}+\cdots +{\vec {F}}\cdot d{\vec {r}}_{n}}$

${\displaystyle (4.2)}$

Deci: lucrul mecanic elementar corespunzător unei deplasări compuse este egal cu suma lucrurilor mecanice elementare aferente deplasărilor componente;

f) dacă forța F reprezintă rezultanta unică a unui sistem de forțe:

${\displaystyle {\vec {F}}={\vec {F}}_{1}+{\vec {F}}_{2}+\cdots +{\vec {F}}_{n}}$

${\displaystyle (4.3)}$

atunci lucrul mecanic este:

${\displaystyle dL={\vec {F}}\cdot d{\vec {r}}={\vec {F}}_{1}\cdot d{\vec {r}}+{\vec {F}}_{2}\cdot d{\vec {r}}+\cdots +{\vec {F}}_{n}\cdot d{\vec {r}}}$

${\displaystyle (4.4)}$

Adică, lucrul mecanic elementar corespunzător rezultantei unui sistem de forțe este egal cu suma algebrică a lucrurilor mecanice elementare ale forțelor componente.

Lucrul mecanic în cazul forțelor conservative

În cazul în care forța F este conservativă, expresia acesteia este:

${\displaystyle {\vec {F}}=\nabla U={\frac {\partial U}{\partial x}}{\vec {i}}+{\frac {\partial U}{\partial y}}{\vec {j}}+{\frac {\partial U}{\partial z}}{\vec {k}}={\mathit {grad}}U,}$

${\displaystyle (5.1)}$

unde ${\displaystyle U(x,y,z)\!}$ este funcția de forță.

Funcția de forță este o funcție scalară de coordonatele punctului, cu ajutorul căreia se pot determina componentele forței astfel:

${\displaystyle {\begin{cases}F_{x}={\frac {\partial U}{\partial x}}\\\\F_{y}={\frac {\partial U}{\partial y}}\\\\F_{z}={\frac {\partial U}{\partial z}}\end{cases}}}$

${\displaystyle (5.2)}$

Pentru a exista o funcție de forță trebuie îndeplinite condițiile lui Cauchy, care sunt :

${\displaystyle {\frac {\partial F_{x}}{\partial y}}={\frac {\partial F_{y}}{\partial x}};\!}$     ${\displaystyle {\frac {\partial F_{y}}{\partial z}}={\frac {\partial F_{z}}{\partial y}};\!}$     ${\displaystyle {\frac {\partial F_{z}}{\partial x}}={\frac {\partial F_{x}}{\partial z}}\!}$

${\displaystyle (5.3)}$

Lucrul mecanic elementar este:

${\displaystyle dL={\vec {F}}\cdot d{\vec {r}}={\frac {\partial U}{\partial x}}dx+{\frac {\partial U}{\partial y}}dy+{\frac {\partial U}{\partial z}}dz=dU}$

${\displaystyle (5.4)}$

${\displaystyle dL=dU}$

${\displaystyle (5.5)}$

Lucrul mecanic total este:

${\displaystyle L_{A-B}=\int _{AB}{\vec {F}}d{\vec {r}}=\int _{A}^{B}dU=U_{B}-U_{A}}$

${\displaystyle (5.6)}$

unde ${\displaystyle U_{A}=U(x_{A},y_{A},z_{A})\!}$ și ${\displaystyle U_{B}=U(x_{B},y_{B},z_{B})\!}$ sunt funcțiile de forță corespunzătoare pozițiilor inițială și finală.

Rezultă că: lucrul mecanic total în cazul unei forțe conservative depinde numai de pozițiile inițială și finală ale punctului, fiind independent de forma traiectoriei. În locul funcției U, se poate considera funcția V, numită și funcție Potențial și definită prin relația: ${\displaystyle V=-U.}$ În acest caz, lucrul mecanic elementar are expresia ${\displaystyle dL=-dV.}$

Funcția de forță U și funcția potențial V nu pot fi determinate decât cu aproximația unei constante.

Dacă un punct material este acționat simultan de un sistem de forțe conservative ${\displaystyle {\vec {F}}_{1},{\vec {F}}_{2},\cdots ,{\vec {F}}_{n}\!}$ care derivă din funcțiile de forță ${\displaystyle U_{1},U_{2},\cdots ,U_{n},\!}$ astfel încât:

${\displaystyle {\begin{matrix}F_{x1}={\frac {\partial U_{1}}{\partial x}}&F_{y1}={\frac {\partial U_{1}}{\partial y}}&F_{z1}={\frac {\partial U_{1}}{\partial z}}\\\\F_{x2}={\frac {\partial U_{2}}{\partial x}}&F_{y2}={\frac {\partial U_{2}}{\partial y}}&F_{z2}={\frac {\partial U_{2}}{\partial z}}\\\\\cdots &\cdots &\cdots \\\\F_{xn}={\frac {\partial U_{n}}{\partial x}}&F_{yn}={\frac {\partial U_{n}}{\partial y}}&F_{zn}={\frac {\partial U_{n}}{\partial z}}\end{matrix}}}$

${\displaystyle (5.7)}$

Rezultanta ${\displaystyle {\vec {R}}={\vec {F}}_{1}+{\vec {F}}_{2}+\cdots +{\vec {F}}_{n}\!}$ va avea proiecțiile:

${\displaystyle F_{x}={\frac {\partial (U_{1}+U_{2}+\cdots +U_{n})}{\partial x}}\!}$ ${\displaystyle F_{y}={\frac {\partial (U_{1}+U_{2}+\cdots +U_{n})}{\partial y}}\!}$ ${\displaystyle F_{z}={\frac {\partial (U_{1}+U_{2}+\cdots +U_{n})}{\partial z}}\!}$

${\displaystyle (5.8)}$

adică rezultanta  ${\displaystyle {\vec {R}}\!}$  derivă din funcția de forță  ${\displaystyle U=U_{1}+U_{2}+\cdots +U_{n}.\!}$ Un astfel de sistem de forțe se numește sistem conservativ.

Cazuri particulare

Lucrul mecanic efectuat de o forță conservativă nu depinde de drumul efectuat de punctul material supus acțiunii acelei forțe, ci numai de pozițiile extreme ale traiectoriei. Exemple de forțe conservative: greutatea, forța elastică, forța electrostatică.

Greutatea

Lucrul mecanic al forței de greutate are expresia:

${\displaystyle L=mgh,}$

${\displaystyle (6.1.1)}$

unde:

• m = masa corpului,
• g = accelerația gravitațională,
• h = diferența de nivel dintre poziția finală și cea inițială a corpului.

De remarcat faptul că h este negativ când corpul urcă, în care caz ${\displaystyle L<0.}$

Forța elastică

Forța elastică ce apare la deformarea unui resort este o forță centrală care are la origine o deformație elastică a unui mediu, proporțională cu deformația x, dar de sens contrar:

${\displaystyle {\vec {\mathbf {F} }}=-k{\vec {\mathbf {x} }}.}$ F=kx

${\displaystyle (6.2.1)}$

Lucrul mecanic al forței elastice atunci când resortul se deformează de la 0 la x este:

${\displaystyle L=\int _{0}^{x}F(x)dxcos\alpha =\int _{0}^{x}(kx)dxcos\alpha =-{\frac {kx^{2}}{2}},\alpha =180}$

${\displaystyle (6.2.2)}$

Deplasarea particulelor electrizate în câmp electric (produs de un condensator)

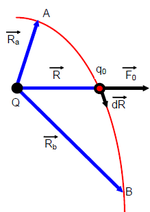
Se consideră câmpul electric generat de sarcina Q, în care se deplasează sarcina sondă ${\displaystyle q_{0}}$.

Lucrul mecanic de origine electrică sau mai exact electrochimică (furnizat de o baterie electrică sau celulă electrochimică^[7]) efectuat de forța electrostatică ce acționează asupra sarcinii sondă este:

${\displaystyle L_{AB}=\int _{A}^{B}{\vec {F_{0}}}\cdot d{\vec {R}}={\frac {1}{4\pi \epsilon }}\int _{A}^{B}{\frac {{\vec {R}}\cdot d{\vec {R}}}{R^{3}}},}$

${\displaystyle (6.3.1)}$

unde

• ${\displaystyle {\vec {R}}=x{\vec {i}}+y{\vec {j}}+z{\vec {k}}=}$ vectorul de poziție al sarcinii ${\displaystyle q_{0}}$, considerate punctuale;
• ${\displaystyle d{\vec {R}}=dx\cdot {\vec {i}}+dy\cdot {\vec {j}}+dz\cdot {\vec {k}}=}$ vectorul deplasare al sarcinii;
• ${\displaystyle \epsilon =}$ permitivitatea mediului.

Rezultă:

${\displaystyle L_{AB}={\frac {Qq_{0}}{4\pi \epsilon }}\int _{A}^{B}{\frac {dR}{R^{2}}}={\frac {Qq_{0}}{4\pi \epsilon }}\left({\frac {1}{R_{a}}}-{\frac {1}{R_{b}}}\right).}$

${\displaystyle (6.3.2)}$

Această formulă servește la definirea diferenței de potențial electric. math> d \vec R = dx \cdot \vec i +dy \cdot \vec j + dz \cdot \vec k=

Formulă dimensională și unități de măsură

Conform analizei dimensionale, formula dimensională pentru lucru mecanic se scrie sub forma:

Adică, dimensiunea fizică a lucrului mecanic este masă ori lungime la pătrat ori timpul la puterea minus doi.

În Sistemul Internațional de Măsuri forța se măsoară în newtoni și lungimea în metri, rezultă că unitatea de măsură pentru lucru mecanic este:

În SI, lucrul mecanic se măsoară deci în joule, notat prin litera J, care este egal cu newton ori metru. Lucrul mecanic de un joule este efectuat de o forță de un newton, atunci când produce o deplasare de un metru a punctului său de aplicație paralel și în același sens cu vectorul forță .

În sistemul de măsuri tolerat, cgs, unitatea de măsură este ${\displaystyle \scriptstyle [L]_{cgs}=[F]_{cgs}[s]_{cgs}=dyn\cdot cm=erg}$, transformarea dintre cele două unități este dată de relația: ${\displaystyle \scriptstyle 1J=10^{7}erg}$ sau reciproc: ${\displaystyle \scriptstyle 1erg=10^{-7}J}$.

Note

Bibliografie

• Șerban Țițeica: Termodinamica, Editura Academiei Republicii Socialiste România, București, 1982.
• George C. Moisil: Termodinamica, Editura Academiei RSR, București, 1988.
• Stoian Petrescu, Valeria Petrescu: Principiile termodinamicii - Evoluție, fundamentări, aplicații, Editura Tehnică, București, 1983
• Eugen Toma: Introducere în astrofizică, Editura Tehnică, București, 1980
• Ion M. Popescu: Fizica - Termodinamica, Editura Politehnica Press, București, 2002
• V. Kirillin, V. Sîcev, A. Șeindlin, Termodinamica, Editura Științifică și Enciclopedică, 1985, (traducere din limba rusă)

Vezi și

• Mecanică clasică
• Momentul forței
• Căldură
• Forță
• Deplasare
• Sistem termodinamic
• Joule