Mecanică lagrangiană

Parte a seriei de articole despre
Mecanică clasică
${\displaystyle {\vec {F}}=m{\vec {a}}}$ Principiul al II-lea al mecanicii
Istorie Cronologie
Ramuri Cinematică Dinamică Mecanică cerească aplicată a mediilor continue statistică Statică
Concepte Accelerație Energie cinetică potențială Forță aparentă frecare Impuls Inerție Lucru mecanic virtual Masă Moment cinetic de inerție Principiul lui D'Alembert Putere Sistem de referință inerțial neinerțial Spațiu Timp Viteză relativă
Formulări Legile lui Newton Mecanică analitică Mecanică lagrangiană Mecanică hamiltoniană Ecuația Hamilton–Jacobi
Subiecte de bază Deplasare Legea atracției universale Mișcare ecuații armonică rectilinie Solid rigid
Rotație Rotație Sistem de referință în rotație Viteză unghiulară Accelerație unghiulară Forță centripetă centrifugă Forța Coriolis Frecvență Oscilație oscilator armonic amortizare Pendul conic Vibrație
Oameni de știință Galileo Huygens Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy
Categorii Mecanică clasică
v d m

Prin Mecanică lagrangiană sau ecuațiile lui Lagrange se înțelege o reformulare a mecanicii newtoniene, formulată întâia oară în anul 1788 de matematicianul Joseph Louis Lagrange. Reformularea presupune caracterizarea unui sistem mecanic printr-o singură funcție scalară numită funcția Lagrange a sistemului sau, mai simplu, lagrangianul sistemului. Analiza acestei funcții permite determinarea ecuațiilor de mișcare ale sistemului care, odată rezolvate, relevă toate informațiile necesare analizei dinamicii sistemului.

Lagrangianul

Într-un sistem cu un potențial de forță generalizat și un număr adecvat de constrângeri, lagrangianul este definit ca

${\displaystyle {\mathcal {L}}=T-V}$

unde ${\displaystyle T}$ este energia cinetică a sistemului, iar ${\displaystyle V}$ cea potențială.

Ecuațiile de mișcare

Pentru a caracteriza integral un sistem mecanic cu ${\displaystyle N}$ grade de libertate și ${\displaystyle k}$ constrângeri independente este nevoie de ${\displaystyle N-k}$ variabile, care se numesc coordonate generalizate și sunt notate cu ${\displaystyle q_{1},q_{2}\ldots q_{N-k}}$. Coordonatele generalizate pot fi asociate cu câte o masă din cadrul sistemului mecanic, notate ${\displaystyle m_{1},m_{2}\ldots m_{N-k}}$.

Energia cinetică totală a sistemului (notată ${\displaystyle T}$) se poate obține deci însumând pătratele vitezelor generalizate (derivatele coordonatelor generalizate după timp, notate ${\displaystyle {\dot {q}}_{1},{\dot {q}}_{2}\ldots {\dot {q}}_{N-k}}$) înmulțite cu jumătatea masei corespunzătoare. Energia potențială poate varia în funcție de natura sistemului mecanic.

${\displaystyle T=\sum _{j}{{\frac {1}{2}}m_{j}{\dot {q}}_{j}^{2}}}$

Prin ecuațiile de mișcare ale sistemului se înțelege atunci un sistem de ${\displaystyle N-k}$ ecuații diferențiale (câte una pentru fiecare coordonată generalizată), formulate astfel:

${\displaystyle {\frac {\text{d}}{{\text{d}}t}}{\frac {\partial {\mathcal {L}}}{\partial {\dot {q}}_{j}}}-{\frac {\partial {\mathcal {L}}}{\partial q_{j}}}=0\,.}$

Ecuațiile mai sunt cunoscute sub numele de ecuațiile Euler-Lagrange și rezultă din aplicarea principiului Hamiltonian, conform căruia fiecare sistem mecanic se dezvoltă în timp în așa chip, încât integrala acțiunii să fie minimală.

Proprietăți ale Lagrangianului

Variabile ciclice și simetrii

Dacă lagrangianul nu depinde explicit de vreo coordonată generalizată ${\displaystyle q_{k}}$, atunci aceasta se numește variabilă ciclică sau coordonată ciclică. Prezența în calcul a unei variable ciclice indică prezența în sistem a unei simetrii. Ecuația de mișcare pentru coordonata ${\displaystyle q_{k}}$ ia atunci forma mai simplă:

${\displaystyle {\frac {\text{d}}{{\text{d}}t}}{\frac {\partial {\mathcal {L}}}{\partial {\dot {q}}_{j}}}=0\,.}$

indicând că acea cantitate notată ${\displaystyle \partial {\mathcal {L}}/\partial {\dot {q}}_{j}}$ (Impulsul asociat coordonatei ${\displaystyle q_{k}}$) este o cantitate conservată. Faptul că orice simetrie continuă a unui sistem rezultă în conservarea unei cantități este enunțul principal al Teoremei lui Noether.

Exemple

Masă aflată într-un potențial de forță armonic (conservativ)

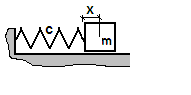
O masă ${\displaystyle m}$ fie conectată prin două arcuri cu constanta de elasticitate ${\displaystyle D}$ la doi pereți ficși. Avem deci o singură coordonată generalizată ${\displaystyle x}$, anume distanța masei de punctul de echilibru. Pentru acest sistem se determină lagrangianul după definiție. ${\displaystyle T}$ este energia cinetică iar ${\displaystyle V}$ cea potențială:

${\displaystyle T={\frac {1}{2}}m{\dot {x}}^{2}}$

${\displaystyle V={\frac {1}{2}}Dx^{2}}$

Lagrangianul este deci diferența:

${\displaystyle L={\frac {1}{2}}m{\dot {x}}^{2}-{\frac {1}{2}}Dx^{2}}$

Se introduce lagrangianul în ecuația de mișcare:

${\displaystyle {d \over dt}{\partial {\mathcal {L}} \over \partial {\dot {x}}}={\partial {\mathcal {L}} \over \partial x}}$

Evaluând expresiile și simplificând avem:

${\displaystyle \ {\frac {\mathrm {d} }{\mathrm {d} t}}\left(m{\dot {x}}\right)=-Dx}$

Se obține deci o ecuație diferențială a mișcării:

${\displaystyle {\ddot {x}}=-{\frac {D}{m}}x}$.

Soluția acestei ecuații diferențiale de gradul al 2-lea se obține prin Ansatz-ul ${\displaystyle x(t)=A\cos(\omega t+\varphi )}$, ${\displaystyle t}$ fiind timpul, iar ${\displaystyle \omega ={\sqrt {D/m}}}$ frecvența oscilării. Amplitudinea constantă ${\displaystyle A}$ și faza ${\displaystyle \varphi }$ pot fi determinate din condițiile inițiale sau marginale ale sistemului.

Bibliografie

• Nolting, Wolfgang, Grundkurs Theoretische Physik 2: Analytische Mechanik [Elektronische Ressource], Springer-Verlag Berlin Heidelberg (2011), ISBN 978-3-642-12950-6
• Moțoc, Cornelia, Fizica. Bazele fizicii clasice, Editura All, 1998