黄金長方形

黄金長方形（おうごんちょうほうけい、英: golden rectangle）とは、縦横の長さの比が黄金比、すなわち

${\displaystyle 1:{\frac {1+{\sqrt {5}}}{2}}\approx 1.618}$

の長方形のことである。

日本で用いられる名刺はこの長方形に近い形状をしている。

黄金長方形から最大の正方形を除くと、残った長方形は元の黄金長方形と相似になる。これを繰り返すと、無数の相似な図形が出来ていく。図のように、正方形の列において角の点を滑らかにつないでいくと、渦巻が出来ていく。この螺旋は、巻貝の貝殻に現れている渦巻きと同種の対数螺旋である。

逆に、内側からフィボナッチ数列を一辺の長さとする正方形を連ねていくと、次第に黄金長方形に近くなる。

ギャラリー

• 
  黄金長方形では、(長辺 - 短辺) : 短辺 = 短辺 : 長辺 が成り立つことを表した図。
• 
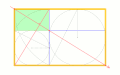  黄金長方形から最大正方形を切り取っていった図（残った長方形も黄金長方形になる）。
• 
  黄金数 φ について、φ(φ − 1) = 1 を、面積で表した図。青線が、縦横の長さ 1, φ の黄金長方形2個を表し、右上の赤網目部分が φ(φ − 1)、左下の赤網目部分が 1 を表す。
• 
  黄金数 φ について、φ(φ − 1) = 1 を、面積で表した図。縦横の長さが 1, φ の黄金長方形（青線）において、斜線部分が等積となる。また、赤網目部分は √5φ = 1 + φ² を表している。
• 
  互いに合同な直角二等辺三角形を図のように並べると黄金長方形が出来る。
• 
  正円とその中心を通る水平並びに傾き２の直線との交点を活用すると図のように黄金長方形（赤・青・緑）を描ける。
• 
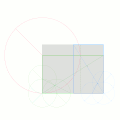  幾何学的に或る長方形（灰色）からその長辺または短辺の全長を使い切った黄金長方形を切り取る方法の一例。（青枠または緑枠で示される長方形が黄金長方形となっている。）
• 
  「半径２の正円」（緑）と「辺の長さが１とφの黄金長方形」（橙）を活用すると図のように当該正円の円周を２０等分する点を求めることができる。
• 
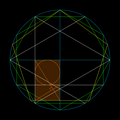  同一の正円(青)に内接する正五角形(黄)と正六角形(緑)を活用して黄金長方形(橙)を作り出す例

関連項目

• 黄金比
• 対数螺旋
• フィボナッチ数
• 黄金三角形

外部リンク

ウィキメディア・コモンズには、黄金長方形に関連するカテゴリがあります。

• Weisstein, Eric W. "Golden Rectangle". mathworld.wolfram.com (英語).

表 話 編 歴 貴金属比
ピゾ数（英語版） 黄金 角 進法 フィボナッチ数列 ケプラー三角形 長方形 菱形（英語版） 分割探索 螺旋 三角形 白銀 ペル数 長方形 青銀 カッパー ニッケル etc...