Moment de inerție polar

Nu confundați cu momentul de inerție, care caracterizează accelerația unghiulară a unui obiect datorită unui moment.

În rezistența materialelor momentul de inerție polar^[1][2][3] este o mărime folosită pentru a descrie rezistența la deformare determinată de torsiune, a obiectelor (sau părților unui obiect) cu o secțiune transversală invariantă și fără deformare semnificativă.^[4] Se poate calcula din momentul de inerție planar, de care este legat prin teorema axei perpendiculare. În timp ce momentul de inerție planar descrie rezistența unui obiect la deformarea prin încovoiere atunci când este supus unei forțe aplicate într-un plan care conține axa sa centrală, momentul de inerție polar descrie rezistența unui obiect la deformare atunci când este supus unui moment paralel cu axa centrală a obiectului (adică perpendicular pe secțiunea transversală). Similar cu momentele planare (${\displaystyle I_{x}}$,${\displaystyle I_{y}}$ și ${\displaystyle I_{xy}}$), momentul de inerție polar al secțiunii este adesea notat prin ${\displaystyle I_{p}}$. În mai multe manuale de inginerie și publicații academice este notat și cu ${\displaystyle I_{z}}$, ${\displaystyle J}$ sau ${\displaystyle J_{z}}$, dar această notație nu trebuie să fie confundată cu constanta de torsiune, ${\displaystyle J_{t}}$ sau ${\displaystyle I_{s}}$, folosită pentru obiecte necilindrice.

Momentul polar al secțiunii este rezistența unui arbore sau a unei bare de a fi deformată prin torsiune, în funcție de forma sa. Cu cât este mai mare momentul de inerție polar, cu atât este mai mare rezistența la torsiune a obiectului. Rezistența provine numai din aria secțiunii transversale a obiectului și nu depinde de compoziția materialului sau de modulul de elasticitate transversal. Acesta din urmă intervine doar asupra mărimii deformației datorită torsiunii.

Definiție

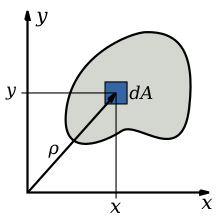
Ecuația care descrie momentul polar al ariei este o integrală multiplă peste aria secțiunii transversale, ${\displaystyle A}$, a obiectului.

${\displaystyle J=\iint _{A}\rho ^{2}\,dA}$

unde ${\displaystyle \rho }$ este distanța până la elementul ${\displaystyle dA}$.

Înlocuind componentele ${\displaystyle x}$ și ${\displaystyle y}$ și folosind teorema lui Pitagora:

${\displaystyle J=\iint _{A}\left(x^{2}+y^{2}\right)dx\,dy}$

${\displaystyle J=\iint _{A}x^{2}\,dx\,dy+\iint _{A}y^{2}\,dx\,dy}$

Fiind date momentele de inerție axiale:

${\displaystyle I_{x}=\iint _{A}y^{2}dx\,dy,}$   respectiv

${\displaystyle I_{y}=\iint _{A}x^{2}dx\,dy,}$

se poate arăta că momentul de inerție polar este suma momentelor de inerție axiale ${\displaystyle I_{x}}$ și ${\displaystyle I_{y}}$^[2][3][5]

${\displaystyle J=I_{p}=I_{x}+I_{y}}$

La obiectele care au simetrie de rotație,^[6] cum ar fi cilindrii sau țevile, relația se simplifică la:

${\displaystyle J=2I_{x}}$   sau   ${\displaystyle J=2I_{y}}$

Pentru o secțiune rotundă cu raza ${\displaystyle R}$:

${\displaystyle I_{z}=\int _{0}^{2\pi }\int _{0}^{R}r^{2}(r\,dr\,d\phi )={\frac {\pi R^{4}}{2}}}$

Unități

Unitatea de măsură în SI pentru momentul de inerție polar este aceeași cu a momentelor de inerție axiale: m⁴.

Limitări

Modulul de inerție polar poate fi insuficient pentru calculul barelor și arborilor cu secțiuni transversale nerotunde, datorită tendinței lor de a se deforma la răsucire, provocând deformații în afara planului secțiunii inițiale. În astfel de cazuri se folosește constanta de torsiune a secțiunii.^[7]

La obiecte la care secțiunea variază considerabil se recomandă metode mai performante, cum ar fi metoda elementelor finite^⁠(d).

Aplicație

Deși momentul de inerție polar al secțiunii este cel mai adesea folosit pentru a calcula deformația unghiulară a unui obiect supus unui moment aplicat perpendicular pe secțiunea transversală, valoarea rigidității la torsiune depinde și de materialul din care este făcut obiectul, mai exact de modulul de elasticitate transversal, ${\displaystyle G}$. Legând aceste două caracteristici de lungimea arborelui, ${\displaystyle L}$, se poate calcula deformarea unghiulară a arborelui, ${\displaystyle \theta }$, datorită momentului aplicat, ${\displaystyle M_{t}}$:

${\displaystyle \theta ={\frac {M_{t}L}{JG}}}$

Deci, cu cât modulul de elasticitate transversal și momentul de inerție polar sunt mai mari, cu atât deformația dată de răsucire este mai mică.

Momentul de inerție polar al secțiunii apare și în formulele pentru tensiunea tangențială dată de torsiune:

${\displaystyle \tau ={\frac {M_{t}\,\rho }{J}}}$

unde ${\displaystyle \rho }$ este distanța de la axa centrală la punctul de interes. Pentru secțiuni circulare tensiunea este maximă la exteriorul secțiunii.

Note

Vezi și

• Constantă de torsiune
• Moment de inerție planar
• Listă de momente de inerție planare
• Modul de elasticitate transversal

Legături externe

	Portal Fizică
	Portal Inginerie mecanică

• en Torsion of Shafts - engineeringtoolbox.com
• en Elastic Properties and Young Modulus for some Materials - engineeringtoolbox.com
• en Material Properties Database - matweb.com