Cerc înscris și cerc exînscris unui triunghi
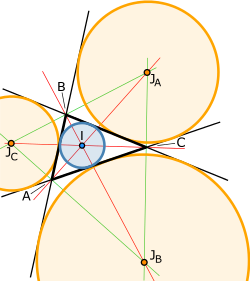
În geometria triunghiului, cercul înscris într-un triunghi și cercurile exînscrise unui triunghi sunt cercuri tangente tuturor laturilor triunghiului sau prelungirilor acestora.
Cercul înscris
Cercul înscris într-un triunghi este acel cerc aflat în interiorul triunghiului la intersecția bisectoarelor și căruia toate laturile triunghiului (considerate segmente), nu prelungirile acestora) îi sunt tangente. Este cel mai mare cerc aflat în interiorul triunghiului.
Centrul cercului înscris într-un triunghi se află la intersecția bisectoarelor unghiurilor acestuia.
Raza cercului înscris se determină cu formulele:
unde sunt lungimile laturilor triunghiului, semiperimetrul, iar aria triunghiului.
Cercul exînscris
Cercul exînscris este tangent doar uneia dintre laturi (considerată ca segment) și prelungirilor celorlalte două. Există trei asemenea cercuri. Astfel, cercul care corespunde vârfului A are centrul în care este situat la intersecția bisectoarei din A cu perpendicularele duse la bisectoarele din B și din C.
Razele cercurilor exînscrise sunt date de:
 | Acest articol referitor la geometrie este deocamdată un ciot. Puteți ajuta wikipedia prin completarea sa! |




















