Grafo regular
| Famílias de grafos definidos por seus automorfismos | ||||
| distância-transitivo | distância-regular | fortemente regular | ||
| simétrico (arco-transitivo) | t-transitivo, t ≥ 2 | . | ||
(se conectado) | ||||
| transitivo nos vértices e nas arestas | aresta-transitivo e regular | aresta-transitivo | ||
| vértice-transitivo | regular | |||
| grafo de Cayley | antissimétrico | assimétrico | ||
Em Teoria dos grafos, um grafo regular é um grafo onde cada vértice tem o mesmo número de adjacências, i.e. cada vértice tem o mesmo grau ou valência. Um grafo direcionado regular também deve satisfazer a condição mais forte de que o grau de entrada e o grau de saída de cada vértice sejam iguais uns aos outros.[1] Um grafo regular com vértices de grau k é chamado um grafo k‑regular ou grafo regular de grau k.
Grafos regulares de grau no máximo 2 são fáceis de classificar: Um grafo 0-regular é composto por vértices desconectados, um grafo 1-regular consiste de arestas desconectadas, e um grafo 2-regular consiste de ciclos desconectados.
Um grafo 3-regular é conhecido como um grafo cúbico.
Um grafo fortemente regular é um grafo regular, onde cada par de vértices adjacentes tem o mesmo número l de vizinhos em comum, e cada par de vértices não-adjacentes tem o mesmo número n de vizinhos em comum. Os menores grafos que são regulares, mas não fortemente regulares são os grafos ciclos e os grafos circulantes em 6 vértices.
O grafo completo é fortemente regular para qualquer .
Um teorema de Nash-Williams diz que cada k‑grafo regular em 2k + 1 vértices tem um ciclo hamiltoniano.
-
 grafo 0-regular
grafo 0-regular -
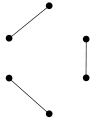 grafo 1-regular
grafo 1-regular -
 grafo 2-regular
grafo 2-regular -
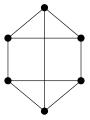 grafo 3-regular
grafo 3-regular
Propriedades algébricas
Seja A a matriz de adjacência de um grafo. Então, o grafo é regular se e somente se é um autovetor de A..[2] Seu autovalor será o grau constante do grafo. Autovetores correspondentes a outros autovalores são ortogonais a , assim como para tais autovetores , nós temos .
Um grafo regular de grau k é conectado se e somente se o autovalor k tem uma multiplicidade 1.[2]
Referências
Ligações externas
- «GenReg». software e dados por Markus Meringer.

























