Feltlinje

En feltlinje er en kurve som på hvert sted har en tangent som er parallell med et gitt vektorfelt. Innen matematikk omtales de som integralkurver for vektorfeltet. I fysikken blir feltlinjer benyttet for å illustrere elektriske og magnetiske felt og for å beskrive strømning av væskepartikler i hydrodynamikken. De kalles da for strømlinjer eller flytlinjer. Gjennom hvert punkt går det kun en slik linje. Desto tettere feltlinjene ligger, desto sterkere er feltstyrken.

Matematisk definisjon

Et vektorfelt v = v(x)  tilordner en vektor v  med komponenter v_k = v_k(x)  til hvert punkt x i et gitt rom. En kurve x = x(s)  med affin parameter s i dette rommet har tangentvektorer t = d x/ds i hvert punkt. Denne kurven beskriver da en feltlinje eller integralkurve hvis

${\displaystyle {d\mathbf {x} \over ds}=\mathbf {v} (\mathbf {x} )}$

I et tredimensjonalt, euklidsk rom gir dette tre førsteordens differensialligninger.^[1] De kan sammenfattes på formen

${\displaystyle {dx \over v_{x}}={dy \over v_{y}}={dz \over v_{z}}}$

Disse ligningene kan noen tilfeller løses eksakt, men man kan alltid finne de resulterende feltlinjene med den ønskete nøyaktighet ved bruk av numerisk integrasjon.

Brukes feltlinjene i forbindelse med strømning av en væske, sier man ofte at de beskriver en «flyt» eller en «fluks» av partikler. Denne betegnelsen tas også noen ganger over til elektromagnetismen hvor man snakker om strømning eller flyt av elektrisk og magnetisk fluks.

Kildefritt felt

Divergensen ∇ ⋅ v  til vektorfeltet sier hvor mye som strømmer ut av et tilstrekkelig lite volum som man tenker seg et eller annet sted i feltet. Er denne positiv, strømmer det mer ut enn kommer inn. Vektorfeltet sies da å innholde en kilde som ligger innenfor volumet. I det motsatte tilfellet med en negativ divergens, ligger det en sluk inni volumet. Feltlinjer starter i en kilde og ender i en sluk. I det spesielle tilfellet at ∇ ⋅v = 0  strømmer det like mye ut som inn i volumet. Er dette tilfelle overalt i rommet, sier man at man har en «kildefri flyt». Feltlinjene er da lukkete kurver.

Det magnetiske fluksfeltet B  er overalt kildefritt. Dette skyldes at det ikke finnes magnetiske monopoler og derfor heller ikke mulige kilder eller sluker for dette feltet. Beskriver feltet v  hastighetsfeltet i fluiddynamikk, sier man at betingelsen ∇ ⋅v = 0  gjelder for en inkompressibel væske. Den har konstant tetthet.^[2]

Virvelfritt felt

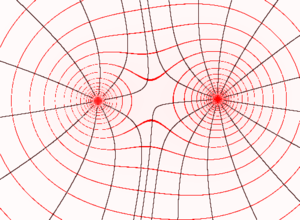
Hvis man på tilsvarende måte plasseres et tilstrekkelig lite møllehjul i hvert punkt i en slik væskestrøm, vil rotasjonen av dette hjulet være gitt ved curl til vektorfeltet ∇ × v. Er denne null overalt, sies flyten å være «virvelfri». Da kan hastighetsfeltet skrives som gradienten av et «hastighetspotensial», det vil si v = ∇ Φ(x)  slik at curl til hastigheten automatisk blir null.

Punkter i rommet med samme potensial, er ekvipotensialflater og er definert ved Φ(x) = konstant. Fra definisjonen står hastighetsvektorene normalt på disse flatene. Flytlinjene skjærer derfor ekvipotensialflatene vinkelrett.

I mekanikken er en konservativ kraft F  definert ved at ∇ × F = 0. Den er derfor virvelfri og er gitt som gradienten til et potensial som i dette tilfellet er den potensielle energien. I elektrostatikken er det elektriske feltet virvelfritt og er gitt ved det elektriske potensialet som E = - ∇ V. De elektriske feltlinjene skjærer derfor alle ekvipotensialflatene under en rett vinkel.

Helmholtz' teorem sier at et vilkårlig vektorfelt i tre dimensjoner kan splittes opp i en del som er kildefri og en del som er virvelfri.^[3]

Eksempler

Det enkleste eksemplet på beregning av feltlinjer kommer fra Coulomb-feltet for en punktladning Q  som kan skrives som

${\displaystyle \mathbf {E} (\mathbf {r} )={Q \over 4\pi \varepsilon _{0}r^{3}}\mathbf {r} }$

hvor posisjonsvektoren r = (x,y,z)  når ladningen ligger i origo. Feltvektorene er rettet i radiell retning. Hvis man betrakter dem i xy - planet, oppfyller komponentene relasjonen E_x /E_y = x/y  slik at differensialligningen for feltlinjene der blir dx/x = dy/y. Direkte integrasjon gir ln x = ln y = konstant. Det betyr at løsningen kan skrives som y = kx  hvor k  er en annen konstant. Feltlinjene er derfor rette linjer ut fra origo. Det er på denne måten Coulomb-feltet vanligvis blir illustrert.

Hvis man i stedet tenker seg et annet felt som har samme størrelse, men hvor for eksempel x - komponenten har motsatt fortegn, vil differensialligningen i xy - planet forandres til dx/x = - dy/y. Den har løsningene y = c/x  hvor c  nå er integrasjonskonstanten. I dette tilfellet er derfor feltlinjene hyperbler med x- og y-aksene som asymptoter.

Magnetisk felt

Det magnetiske feltet er alltid kildefritt. Et enkelt eksempel er feltet fra en uendelig lang og rett ledning som fører en strøm I. Ligger den langs z-aksen, er feltet gitt fra Biot-Savarts lov som

${\displaystyle \mathbf {B} (\mathbf {r} )={\mu _{0}I \over 2\pi r^{2}}\mathbf {k} \times \mathbf {r} }$

hvor k  er en enhetsvektor langs z-aksen.^[3] Ved derivasjon finner man da som forventet at ∇ ⋅B = 0. Feltlinjene er derfor lukkete kurver.

I xy - planet er forholdet mellom feltkomponentene B_x /B_y = -y/x. Herav følger differensialligningen for feltlinjene xdx = -ydy. Ved direkte integrasjon gir den x² + y² = R²  hvor R  igjen er en integrasjonskonstant. Feltlinjene er derfor sirkler med sentrum på z-aksen.

Magnetfeltet kan ikke skrives som gradienten av et skalart potensial slik som det elektriske feltet kan. Derfor kan man heller ikke uten videre tenke seg potensialflater for dette vektorfeltet. Derimot er feltet gitt som curl av et magnetisk vektorpotensial. Kalles dette for A, kan man da alltid skrive at B = ∇ × A. Det gjelder også når feltene varierer med tiden.

Todimensjonal potensialstrømning

Beregning av feltlinjer i todimensjonale systemer er matematisk interessant med mange praktiske anvendelser. Spesielt gjelder det når vektorfeltet er virvelfritt slik at det kan utledes fra et potensial. I hydrodynamikken kalles dette ofte for φ  slik at hastighetsfeltet kan skrives som v = ∇ φ. Komponentene er derfor gitt som

${\displaystyle v_{x}={\partial \phi \over \partial x},\;\;\;v_{y}={\partial \phi \over \partial y}}$

Hvis vektorfeltet i tillegg beskriver en inkompressibel væske, sier man at man har en potensialstrømning. Denne ekstra betingelsen ∇ ⋅v = 0  betyr da at hastighetspotensialet tilfredsstiller den todimensjonale Laplace-ligningen

${\displaystyle {\partial ^{2}\phi \over \partial x^{2}}+{\partial ^{2}\phi \over \partial y^{2}}=0}$

Løsningen er derfor en harmonisk funksjon.

Strømningspotensial

Feltlinjene kan finnes ved å innføre et strømningspotensial ψ(x,y) (også kjent som en strømfunksjon når man snakker om vilkårlige kildefrie felt som ikke nødvendigvis er virvelfrie) definert slik at

${\displaystyle v_{x}={\partial \psi \over \partial y},\;\;\;v_{y}=-{\partial \psi \over \partial x}}$

På den måten blir betingelsen ∇ ⋅v = 0  automatisk oppfylt, ettersom den partiellderiverte av en funksjon ψ med hensyn på y og deretter x, er den samme som den partiellderiverte med hensyn på x og deretter y. Altså ser vi hvorfor kildefrihet er en nødvendig betingelse for at vi skal kunne lykkes med å finne en slik ψ .

Langs en bestemt strømlinje y = y(x)  gjelder da

${\displaystyle {d\psi \over dx}={\partial \psi \over \partial x}+{\partial \psi \over \partial y}{dy \over dx}=-v_{y}+v_{x}{dy \over dx}=0}$

som følger fra den generelle definisjonen av feltlinjer. Dette betyr at de finnes fra strømningspotensialet ved ligningen ψ(x,y) = C  for hver verdi av konstanten C.^[2]

Fra definisjonen av dette nye potensialet ser man at det er relatert til det vanlige hastighetspotensialet ved Cauchy-Riemanns ligninger,

${\displaystyle {\partial \psi \over \partial y}={\partial \phi \over \partial x},\;\;\;{\partial \psi \over \partial x}=-{\partial \phi \over \partial y}}$

Strømningspotensialet oppfyller derfor også Laplace-ligningen. I tillegg betyr det også at begge potensialene inngår i et komplekst potensial

${\displaystyle f(z)=\phi (x,y)+i\psi (x,y)}$

som er en funksjon av den ene variable z = x + iy  hvor i = √-1  er den imaginære enhet. Det er denne sammenhengen med komplekse funksjoner som gjør potensialstrømning i to dimensjoner så matematisk interessant og som også tillater mer direkte beregninger av de tilsvarende feltlinjene.^[4]

Eksempel

Mer kompliserte strømningsforløp i to dimensjoner kan bygges ven kombinasjon av strømninger fra enkle kilder og sluk som for elektromagnetiske felt. Da beskriver det komplekse potensialet

${\displaystyle f(z)={K \over 2\pi }\ln z}$

hvor K  er en reell konstant, en enkelt punktkilde i origo.^[4] Dette kommer tydeligere frem ved bruk av polarkoordinater (r,θ). Da er x = r cosθ  og y = r sinθ  slik at z = r e^iθ. Hastighetspotensialet er derfor

${\displaystyle \phi ={K \over 2\pi }\ln r}$

på samme måte som Coulomb-potensialet i to dimensjoner. Ekvipotensiallinjene er sirkler om origo slik at strømningen er rettet i radiell retning. Hastigheten i denne retningen v_r = ∂φ/∂r  avtar som 1/r  i analogi med det elektriske feltet utenfor en linjeladning.

På samme måte ser man at strømningspotensialet for denne punktkilden er

${\displaystyle \psi ={K \over 2\pi }\theta }$

De tilsvarende feltlinjene er derfor gitt ved θ = konstant. Som forventet er de rette linjer ut fra origo med en konstant verdi for den polare vinkelen.

Se også

• Gradient
• Ekvipotensialflate

Referanser