 6つの双曲線関数 (sinh, cosh, tanh, coth, sech, csch) のグラフ
6つの双曲線関数 (sinh, cosh, tanh, coth, sech, csch) のグラフ 数学において、双曲線関数(そうきょくせんかんすう、英: hyperbolic function)とは、三角関数と類似の関数で、標準形の双曲線を媒介変数表示するときなどに現れる。
概要
 斜線の領域の面積が θ/2 のとき、単位円周上の座標が (cos θ, sin θ) となる。
斜線の領域の面積が θ/2 のとき、単位円周上の座標が (cos θ, sin θ) となる。  斜線の領域の面積が θ/2 のときの双曲線上の座標が (cosh θ, sinh θ)
斜線の領域の面積が θ/2 のときの双曲線上の座標が (cosh θ, sinh θ) 三角関数は単位円周を用いて定義することができる。
- 以下、説明を簡単にするために第一象限(x ≥ 0 かつ y ≥ 0)の議論に限る。
単位円周上の点 A (cos θ, sin θ) と x軸上の点 B(1, 0)、原点 O を考える。線分 AO, BO と弧 AB によって囲まれた領域の面積は θ/2 である。
この性質を用いて逆に三角関数を定義することもできる。すなわち、単位円周上の点 A と x軸上の点 B(1, 0) を取り、線分 AO, BO と弧 AB によって囲まれた領域の面積が θ/2 であるとき、A の座標を (cos θ, sin θ) として、三角関数を定義することができる。
単位円の定義式は

であり、標準形の双曲線の定義式は y2 の符号を変えただけの

である。単位円の面積で三角関数を定義したのと同じように双曲線を用いて双曲線関数を定義することができる。
標準形の双曲線上の点 A と x軸上の点 B(1, 0) を取り、線分 AO, BO と双曲線の囲む領域の面積が θ/2 であるとき、A の座標を (cosh θ, sinh θ) として、双曲線関数 cosh, sinh が定義される。
ちなみに、三角関数の定義に現れた θ は、弧度法における角度に対応していたが、双曲線関数では角度には対応しない。
このように三角関数と双曲線関数は非常に似通った関数として定義され、いろいろな場面でその類似性が現れる。定義に双曲線を用いる関数を双曲線関数と呼ぶことに合わせて、定義に単位円を用いる三角関数を円関数 (circular function) と呼ぶこともある。
定義
双曲線関数は指数関数 ex を用いて

と定義される。sinh, cosh をそれぞれ双曲線正弦関数 (hyperbolic sine; ハイパボリックサイン)、双曲線余弦関数 (hyperbolic cosine; ハイパボリックコサイン) と呼ぶ。他にも三角関数との類似で双曲線正接・余接関数

や、双曲線正割・余割関数

も定義できる。また、例えば cosh を cos hyp や  などと表すこともあり cosech は長いので csch と書くこともある。
などと表すこともあり cosech は長いので csch と書くこともある。
このように定義された、双曲線正弦関数、双曲線余弦関数、双曲線正接関数、双曲線余接関数、双曲線正割関数、双曲線余割関数を総称して双曲線関数という。
指数関数 ex は x を複素変数に拡張できるので、指数関数で定義されている双曲線関数自体も x を複素変数にとってもよい。
双曲線関数はいずれも名称が長いため、読むときは省略されて、sinh はシャインあるいはシンチ[1]、cosh はコッシュ[1]あるいはコシャイン、tanh はタンチ[1]とも読まれる。
記号としての sinh, cosh , tanh はヨハン・ハインリヒ・ランベルトが導入した[2]。
性質
基本性質
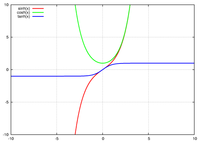 sinh, cosh と tanh のグラフ。特に cosh x のグラフは懸垂線として知られている。
sinh, cosh と tanh のグラフ。特に cosh x のグラフは懸垂線として知られている。  csch, sech と coth のグラフ
csch, sech と coth のグラフ 指数関数を偶関数の部分と奇関数の部分に分けたとき、

となり、偶関数部分が cosh x で、奇関数部分が sinh x であることが分かる。 また (cosh x, sinh x) は、双曲線 x2 − y2 = 1 上の点であり

が成り立つ。
加法定理
三角関数の場合と同様に次の加法定理が成立する[1]。

微分公式

したがって、sinh x と cosh x はいずれも二階の線型微分方程式

の解であり、この微分方程式の基本解系の一つになる。
冪級数展開
双曲線関数のテイラー展開あるいはローラン展開は、以下の式で与えられる。ただし、Bn, En はそれぞれベルヌーイ数 (B2 = 1/6, B4 = −1/30, …)、オイラー数 (E0 = 1, E2 = −1, …) である。
![{\displaystyle {\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\dotsb \\[1ex]\cosh x&=\sum _{n=0}^{\infty }{x^{2n} \over (2n)!}=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\dotsb \\[1ex]\tanh x&=\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\dotsb ,\quad |x|<{\frac {\pi }{2}}\\[1ex]\operatorname {csch} x&={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}}={\frac {1}{x}}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\dotsb ,\quad 0<|x|<\pi \\[1ex]\operatorname {sech} x&=\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}}=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\dotsb ,\quad |x|<{\frac {\pi }{2}}\\[1ex]\coth x&={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}}={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\dotsb ,\quad 0<|x|<\pi \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/498d9c253b18f37825ec849ac3e817f68f94210d)
無限乗積展開
双曲線関数は以下に示す無限乗積に展開される。(→証明)

三角関数との関係
複素変数で定義された三角関数と双曲線関数を比べてみると

という関係にある。
これは、それぞれの指数関数による表現の比較、テイラー展開の比較などによって導出することができる。
逆双曲線関数
双曲線関数が指数関数で表せるように、その逆関数である逆双曲線関数は対数関数を用いて表示することができる。等式 x = sinh y や x = cosh y などを考えれば、これらは ey に関する二次方程式であるから解くことができて、次の表示を得る。

逆関数 sinh−1, cosh−1 などはそれぞれ area sin hyp, area cos hyp (area は「面積」の意)もしくはそれを略して ar sinh, ar cosh と書いたり、逆三角関数と同様に arcsinh, arccosh などと書いたりすることもある。
微分公式

このことから、(1 − x2)1/2 を含む有理関数の原始関数を求めるために x = sin t などと三角関数を用いた置換積分を考えると有用である場合が多いのと同様に、(x2 + 1)1/2 を含む有理関数の積分に双曲線関数を用いた置換積分を考えることは有用であることが多い。
-
arcsinh のグラフ
-
arccosh のグラフ
-
arctanh のグラフ
脚注
[脚注の使い方]
- ^ a b c d 和達三樹『物理のための数学』(新装版)岩波書店〈物理入門コース〉、2017年、18, 232頁。ISBN 978-4-00-029870-4。
- ^ 黒木哲徳『なっとくする数学記号』講談社〈ブルーバックス〉、2021年、146頁。ISBN 9784065225509。
関連項目
外部リンク
- 『双曲線関数(sinh,cosh,tanh)の意味・性質・楽しい話題まとめ』 - 高校数学の美しい物語
- Weisstein, Eric W. "Hyperbolic functions". mathworld.wolfram.com (英語).
典拠管理データベース: 国立図書館  | - フランス
- BnF data
- イスラエル
- アメリカ
- 日本
- チェコ
|
|---|





 arcsinh のグラフ
arcsinh のグラフ arccosh のグラフ
arccosh のグラフ arctanh のグラフ
arctanh のグラフ












![{\displaystyle {\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\dotsb \\[1ex]\cosh x&=\sum _{n=0}^{\infty }{x^{2n} \over (2n)!}=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\dotsb \\[1ex]\tanh x&=\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\dotsb ,\quad |x|<{\frac {\pi }{2}}\\[1ex]\operatorname {csch} x&={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}}={\frac {1}{x}}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\dotsb ,\quad 0<|x|<\pi \\[1ex]\operatorname {sech} x&=\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}}=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\dotsb ,\quad |x|<{\frac {\pi }{2}}\\[1ex]\coth x&={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}}={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\dotsb ,\quad 0<|x|<\pi \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/498d9c253b18f37825ec849ac3e817f68f94210d)












