分離超平面定理

分離超平面定理の概略図。

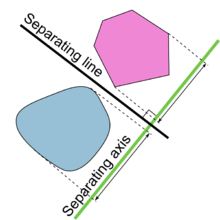
分離超平面定理（ぶんりちょうへいめんていり、英: separating hyperplane theorem, hyperplane separation theorem）は n 次元ユークリッド空間上の互いに素な凸集合に関する幾何学における 2 つの定理を指す。

一つ目の定理は、互いに素な凸集合の両方が閉集合であってかつ少なくともいずれか 1 つの凸集合がコンパクト集合である場合、2 つの閉凸集合の間に 1 つの超平面が存在でき、また閉凸集合の間に 2 つの平行な超平面を隙間を作って置くことができることを示す。

二つ目の定理は、互いに素な凸集合があり両者が開集合である場合、2 つの開凸集合の間に 1 つの超平面をはさむことができるが、2 つの開凸集合の間には必ずしも隙間が存在するわけではないことを示す（従って第一の定理と異なり、複数の超平面を重ねずに挟むことができない状況が存在する）。

分離超平面に対して直交する軸を分離軸 (separating axis) と呼ぶ。これは、2 つの凸体（英語版）の分離軸への直交写像が互いに素であることによる。

分離超平面定理はヘルマン・ミンコフスキーの寄与によって発見された。ハーン＝バナッハの分離定理はミンコフスキーの結果を線型位相空間へ一般化したものである。

関連する結果として支持超平面定理（英語版）がある。マージン最大化超平面 (maximum-margin hyperplane) は空間上にある点の集まりを 2 つのクラスタに分離する超平面の中で、両者のクラスタからの距離が等しいようなものである。このとき、それぞれのクラスタと分離超平面の間のマージンは最大化される。この事実はサポートベクターマシンなどに応用される。

ステートメントと証明

分離超平面定理[1] ― A と B をそれぞれ Rn の互いに素な空でない凸部分集合であるとする。そのような集合について、すべての A の元 x ∈ A と B の元 y ∈ B の組に対して

⟨ x , v ⟩ ≥ c  and  ⟨ y , v ⟩ ≤ c {\displaystyle \langle x,v\rangle \geq c\,{\text{ and }}\langle y,v\rangle \leq c}

を満たす零でないベクトル v と実数 c が存在する。つまり、v を法線ベクトルとする超平面 〈·, v〉 = c によって A と B を分離できる。

証明は以下の補題に基づく：

補題 ― K を Rn の空でない閉凸部分集合とする。集合 K について、K 上の最小ノルムを持つベクトルが一意に存在する。

補題の証明：

K 上のベクトル x のノルムの下限を δ = inf{|x| | x ∈ K} とする。|xj| → δ となるような K 上の数列 xj について、K の凸性より |xi + xj|/2 ∈ K が成り立つ。また、

| x i + x j 2 | ≥ inf { | x | } = δ {\displaystyle \left|{\frac {x_{i}+x_{j}}{2}}\right|\geq \inf\{|x|\}=\delta }

であることから

| x i − x j | 2 = 2 | x i | 2 + 2 | x j | 2 − | x i + x j | 2 ≤ 2 | x i | 2 + 2 | x j | 2 − 4 δ 2 {\displaystyle |x_{i}-x_{j}|^{2}=2|x_{i}|^{2}+2|x_{j}|^{2}-|x_{i}+x_{j}|^{2}\leq 2|x_{i}|^{2}+2|x_{j}|^{2}-4\delta ^{2}}

が得られる。上記の関係について極限を取れば右辺は 0 となり、従って

| x i − x j | ≤ 0 {\displaystyle |x_{i}-x_{j}|\leq 0}

を満たす。すなわち xi はコーシー列であり、Kは完備であるからその極限値は K に含まれるので、δ はベクトル x ∈ K の最小ノルムとなる。最小ノルムを持つベクトルの一意性について、ベクトル y ∈ K が最小ノルム δ を持つならば、

| x − y | 2 ≤ 2 | x | 2 + 2 | y | 2 − 4 δ 2 = 0 {\displaystyle |x-y|^{2}\leq 2|x|^{2}+2|y|^{2}-4\delta ^{2}=0}

となるから x = y である。□

定理の証明：

互いに素な空でない凸集合 A, B が与えられるとして、次のようなミンコフスキー和（英語版）を考える。

K = A + ( − B ) = { x − y ∣ x ∈ A , y ∈ B } . {\displaystyle K=A+(-B)=\{x-y\mid x\in A,y\in B\}.}

B は凸なので −B もまた凸である。A と −Bの（したがって B の）凸性から上記のミンコフスキー和 K は凸である。

K の閉包 K は凸なので、先に示した補題より K について最小ノルムを持つベクトル v が一意に定まる。K の凸性から、任意のベクトル u ∈ K について、線分

v + t ( u − v ) , 0 ≤ t ≤ 1 {\displaystyle v+t(u-v),\,0\leq t\leq 1}

上の点はすべて K に含まれるため、閉包 K のベクトルのノルムについて以下の関係が成り立つ。

| v | 2 ≤ | v + t ( u − v ) | 2 = | v | 2 + 2 t ⟨ v , u − v ⟩ + t 2 | u − v | 2 , ( 0 ≤ t ≤ 1 ) . {\displaystyle |v|^{2}\leq |v+t(u-v)|^{2}=|v|^{2}+2t\langle v,u-v\rangle +t^{2}|u-v|^{2},\quad (0\leq t\leq 1).}

この関係より直ちに次の結果が得られる：

0 ≤ 2 ⟨ v , u ⟩ − 2 | v | 2 + t | u − v | 2 , ( 0 < t ≤ 1 ) . {\displaystyle 0\leq 2\langle v,u\rangle -2|v|^{2}+t|u-v|^{2},\quad (0<t\leq 1).}

更に、t について t → 0 の極限を取れば上記の関係は

⟨ v , u ⟩ ≥ | v | 2 {\displaystyle \langle v,u\rangle \geq |v|^{2}}

と書き換えられる。従って、任意の x ∈ A および y ∈ B について、

⟨ v , x − y ⟩ ≥ | v | 2 {\displaystyle \langle v,x-y\rangle \geq |v|^{2}}

が成り立つ。

ベクトル v が零ベクトルでないならば、この関係より

inf x ∈ A ⟨ x , v ⟩ ≥ | v | 2 + sup y ∈ B ⟨ y , v ⟩ {\displaystyle \inf _{x\in A}\langle x,v\rangle \geq |v|^{2}+\sup _{y\in B}\langle y,v\rangle }

を得て証明を終わる。

反例と一意性

定理の適用できないケース：一方（または両方）の集合が凸でない

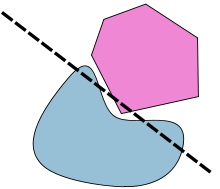
A または B の一方が凸集合でない場合、「分離定理」に対しては様々な反例が挙げられる。例えば A と B は同心円状にとることができる。

より微妙な反例として、A と B の両方が閉凸集合だがいずれもコンパクトでない場合が挙げられる。例として、A が閉半平面で B が双曲線の分枝の一方であるとすれば、この場合には分離超平面は厳密には存在しない（しかしながら、開凸集合に関する分離定理があるために A および B の内部を分離する超平面が 1 つ存在する）：

A = { ( x , y ) : x ≤ 0 } {\displaystyle A=\{(x,y):x\leq 0\}}
B = { ( x , y ) : x > 0 , y ≥ 1 / x } .   {\displaystyle B=\{(x,y):x>0,y\geq 1/x\}.\ }

他のタイプの反例として A がコンパクトな閉凸集合であり B が開凸集合である場合がある。例えば、A を正方形の閉集合、B を正方形の開集合として A と B が接している状況がこれに当てはまる。

閉凸集合に関する分離定理では分離超平面を一意に決めることができないことは明らかである。開集合バージョンの分離定理では、超平面が一意に定まる場合もあるしそうでない場合もあり得る。技術的なことだがこれらのことは分離軸について言い換えられる。閉凸集合の分離定理では分離軸を一意に決められないが、開凸集合の分離定理では分離軸を一意に決定できる。

衝突判定への応用

関連項目

  • 双対錐
  • ファルカスの補題（英語版）

脚注

  1. ^ Boyd & Vandenberghe 2004, Exercise 2.22..

参考文献

  • Boyd, Stephen P.; Vandenberghe, Lieven (2004) (pdf). Convex Optimization. Cambridge University Press. ISBN 978-0-521-83378-3. http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf 
  • Golshtein, E. G.; Tretyakov, N.V. (1996). Modified Lagrangians and monotone maps in optimization. New York: Wiley. p. 6. ISBN 0-471-54821-9 
  • Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Nondifferentiable and two-level mathematical programming. Boston: Kluwer Academic Publishers. p. 19. ISBN 0-7923-9821-1 

外部リンク

  • Collision detection and response