ブレゼンハムのアルゴリズム

ブレゼンハムのアルゴリズム(Bresenham's line algorithm)は、与えられた始点と終点の間に連続した点を置き、近似的な直線を引くためのアルゴリズム。ブレゼンハムの線分描画アルゴリズム、ブレゼンハムアルゴリズムとも。コンピュータのディスプレイに直線を描画するのによく使われ、整数の加減算とビットシフトのみで実装できるので多くのコンピュータで使用可能である。コンピュータグラフィックスの分野の最初期のアルゴリズムの1つである。これを若干拡張すると、円を描くことができる。

アンチエイリアスをサポートした直線描画アルゴリズム（例えば、Xiaolin Wu's line algorithm）もあるが、ブレゼンハムのアルゴリズムの高速性と単純さは今も重要である。プロッターやビデオカードのGPUといったハードウェアで使用されている。ソフトウェアでは多くのグラフィックスライブラリ（英語版）で使用している。非常に単純なので、ビデオカードのファームウェアなどに実装されていることが多い。

歴史

1962年、IBMのジャック・ブレゼンハムが開発した。2001年、ブレゼンハムは次のように記している^[1]。

当時私はサンノゼのIBMの開発研究室で働いていた。Calcomp製プロッター (Calcomp plotter)  が1407タイプライター型コンソール経由で IBM 1401 に接続されていた。このアルゴリズムは1962年夏には使われており、開発したのは1カ月ほど前だったかもしれない。当時プログラムは無償で交換されるものだったので、Calcomp（Jim Newland と Calvin Hefte）もそのコピーを持っていた。1962年秋、私がスタンフォードに戻ったときもコピーをスタンフォードの計算センターのライブラリに入れた。

この直線描画ルーチンについて、1963年コロラド州デンバーで開催されたACM全国大会で発表した。ただし、その年は発表内容が出版されることはなく、単に日程表などに私の発表の題名が掲載されただけだった。その後IBMの Systems Journal が発表した論文を掲載したいと申し出てきたので、よろこんで提供し、1965年に出版された。

ブレゼンハムのアルゴリズムは後に修正を加えられ、円を描画するアルゴリズムにもなっている。こちらのアルゴリズムは midpoint circle algorithm などと呼ばれている。

アルゴリズム

以下が成り立つものとして説明していく。

• 左上端が原点 (0,0) で、ピクセルの座標は右方向と下方向に向かって大きくなる（例えば、(7,4) という座標のピクセルは (7,5) という座標のピクセルに接して上にある）。
• 各ピクセルの中心が、その整数座標に正確に対応するものとする。

いま、x が横方向、y が縦方向の座標であるとして、直線の両端のピクセルの座標が (x₀, y₀) と (x₁, y₁) として与えられたとする。

まず、1つの象限のみを対象とし、線分は右下に向かう方向のみ（すなわち、x₀≤x₁ かつ y₀≤y₁）で、その傾きは1未満（すなわち、${\displaystyle x_{1}-x_{0}}$ の方が ${\displaystyle y_{1}-y_{0}}$ より長い）の場合に限って説明する。この場合、${\displaystyle x_{0}}$ と ${\displaystyle x_{1}}$ の間の x のそれぞれの位置について、（このアルゴリズムでの計算で） y の位置が一意に定まり、${\displaystyle y_{0}}$ と ${\displaystyle y_{1}}$ の間の y のそれぞれの位置には複数のピクセルが描画されうることになる。

ブレゼンハムのアルゴリズムでは、x に対応した y の値（小数値）を計算し、それに最も近い整数値を描画すべきピクセルの座標とする。したがって、1つ前の x で求めた y の整数値と同じか、または1だけ増加することになる。描画すべき線分の方程式は次のようになる。

${\displaystyle {\frac {y-y_{0}}{y_{1}-y_{0}}}={\frac {x-x_{0}}{x_{1}-x_{0}}}}$

x を順次与えて y を求め、最も近い整数値にするので、この式を次のように変形する。

${\displaystyle y={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x-x_{0})+y_{0}}$

傾き ${\displaystyle (y_{1}-y_{0})/(x_{1}-x_{0})}$ は線分の両端の座標のみから求められるので事前に計算しておくことができる。x を順次増やして y を求めるが、最初の値は ${\displaystyle y_{0}}$ であり、それに傾きを繰り返し加算すればよいことになる。

実際には傾きを加算し続けると精度が悪くなる（カハンの加算アルゴリズム参照）。しかし y を整数値に丸めた値と傾きを加算し続けた値の差のみを保持するようにすれば、その値は -0.5 から 0.5 の間で変化するだけであり、精度は悪くならない。すなわち、x を1ずつ増加させ、差に傾きを加算した結果が 0.5 を超えたら y をインクリメントして差から1を引けばよい。

以下の擬似コードでは、plot(x,y) でピクセル描画を行い、abs は絶対値を返すものとする。

 function line(x0, x1, y0, y1)
     int deltax := x1 - x0
     int deltay := y1 - y0
     real error := 0
     real deltaerr := abs (deltay / deltax)    // deltax != 0 と仮定（垂直な線は扱わない）
           // この除算は分数を保持する形で行う必要がある。
     int y := y0
     for x from x0 to x1
         plot(x,y)
         error := error + deltaerr
         if error ≥ 0.5 then
             y := y + 1
             error := error - 1.0

最適化

この技法の問題は、error や deltaerr が分数であるためコンピュータでは計算が遅くなる点であり、さらに浮動小数点数を使った場合は加算によって誤差が蓄積していく点である。整数のみを使った方が高速化され正確になる。そこで上の例で分数または小数になっている全ての数（定数0.5も含む）に deltax をかけて整数にするという技法を使う。ただしそうするとメインループ内で除算が必要になる。そのため error の初期値を変更し、初期値を0として0.5を越えるまでカウントアップするのではなく、初期値を0.5（に deltax をかけた値）にし、0になるまでカウントダウンするように変更する。新たなプログラムの擬似コードは次のようになる。

 function line(x0, y0, x1, y1)
     boolean steep := abs(y1 - y0) > abs(x1 - x0)
     if steep then
         swap(x0, y0)
         swap(x1, y1)
     if x0 > x1 then
         swap(x0, x1)
         swap(y0, y1)
     int deltax := x1 - x0
     int deltay := abs(y1 - y0)
     int error := deltax / 2
     int ystep
     int y := y0
     if y0 < y1 then ystep := 1 else ystep := -1
     for x from x0 to x1
         if steep then plot(y,x) else plot(x,y)
         error := error - deltay
         if error < 0 then
             y := y + ystep
             error := error + deltax

なお、このプログラムは (x0, y0) と (x1, y1) の位置関係がどうであっても描画できるようにしているが、基本形と逆転していると描画順序が反転する。破線を描く場合など描画順序が重要な場合、2つめのswapを排除して次のように簡略化する必要がある。

function line(x0, y0, x1, y1)
     boolean steep := abs(y1 - y0) > abs(x1 - x0)
     if steep then
         swap(x0, y0)
         swap(x1, y1)
     int deltax := abs(x1 - x0) // 修正
     int deltay := abs(y1 - y0)
     int error := deltax / 2
     int ystep
     int y := y0
  
     int inc // 追加
     if x0 < x1 then inc := 1 else inc := -1 // 追加
 
     if y0 < y1 then ystep := 1 else ystep := -1
     for x from x0 to x1 with increment inc // 修正
         if steep then plot(y,x) else plot(x,y)
         // increment により描画順序が制御される
         error := error - deltay
         if error < 0 then
             y := y + ystep
             error := error + deltax

単純化

誤差を両方向同時に計算すれば、初期化部分の swap を排除できる。

 function line(x0, y0, x1, y1)
   dx := abs(x1-x0)
   dy := abs(y1-y0) 
   if x0 < x1 then sx := 1 else sx := -1
   if y0 < y1 then sy := 1 else sy := -1
   err := dx-dy
 
   loop
     setPixel(x0,y0)
     if x0 = x1 and y0 = y1 exit loop
     e2 := 2*err
     if e2 > -dy then 
       err := err - dy
       x0 := x0 + sx
     end if
     if e2 <  dx then 
       err := err + dx
       y0 := y0 + sy 
     end if
   end loop

導出

ブレゼンハムのアルゴリズムは2段階で導出される。第一段階は傾きを係数とする通常の直線の方程式を別の形式に変換するものである。そして、その新しい方程式を使い、誤差の累積という考え方に基づいて直線を描画する。

直線の方程式

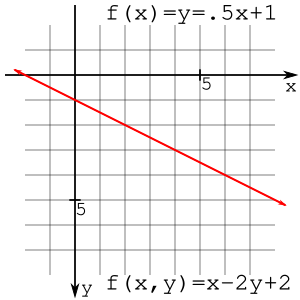
傾きを係数とする直線の方程式は次のとおりである。

${\displaystyle y=f(x)=mx+b}$

ここで m が傾き、b がy軸上の値（y軸との交点）である。この方程式は x についての関数だが、これを x と y の関数に変換することで扱いやすくする。傾きを ${\displaystyle \Delta y/\Delta x}$ と表し、代数学的変換を施す。

${\displaystyle {\begin{aligned}y&=mx+b\\y&={\frac {(\Delta y)}{(\Delta x)}}x+b\\(\Delta x)y&=(\Delta y)x+(\Delta x)b\\0&=(\Delta y)x-(\Delta x)y+(\Delta x)b\end{aligned}}}$

この最後の式を x と y の関数として次のように表せる。

${\displaystyle f(x,y)=0=Ax+By+C}$

ここで、各定数は次の通り。

• ${\displaystyle A=\Delta y}$
• ${\displaystyle B=-\Delta x}$
• ${\displaystyle C=(\Delta x)b}$

この場合、直線はA、B、Cという定数で定義され、${\displaystyle f(x,y)=0}$ となる点の集合となる。直線上にない任意の座標 ${\displaystyle (x,y)}$ では ${\displaystyle f(x,y)\neq 0}$ となる。x と y が整数しかとらないなら、定数も全て整数で表され、この式には整数しか関与しないことになる点が重要である。

例えば ${\displaystyle y={\frac {1}{2}}x+1}$ で表される直線は、${\displaystyle f(x,y)=x-2y+2}$ と書くこともできる。点 (2,2) はこの直線上にある。

${\displaystyle f(2,2)=x-2y+2=(2)-2(2)+2=2-4+2=0}$

また、点 (2,3) は直線上にはない。

${\displaystyle f(2,3)=(2)-2(3)+2=2-6+2=-2}$

点 (2,1) も同様である。

${\displaystyle f(2,1)=(2)-2(1)+2=2-2+2=2}$

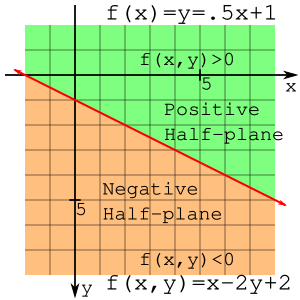
(2,1) と (2,3) はこの直線をはさんで反対側にあり、どちら側になるかは f(x,y) の値が正か負かで決まる。すなわち、直線は平面を2つの半平面に分割するものであり、f(x,y) が負になる半平面と正になる半平面が存在する。この性質はアルゴリズムの導出において重要である。

アルゴリズム

線分の始点は明らかに直線上にある。

${\displaystyle f(x_{0},y_{0})=0}$

この場合、直線は始点と終点を整数座標で指定することで定義される。

傾きは1以下なので、問題は次の点を ${\displaystyle (x_{0}+1,y_{0})}$ と ${\displaystyle (x_{0}+1,y_{0}+1)}$ のどちらにすべきかということに帰結する。直観的には ${\displaystyle x_{0}+1}$ のときの直線の通る位置がどちらの点に近いかで選択すればよい。そこで、2点の中間点を考える。

${\displaystyle f(x_{0}+1,y_{0}+1/2)}$

の計算結果が負なら中間点は直線より下にあり、正なら中間点は直線より上にある。中間点が直線より下なら、直線は ${\displaystyle (x_{0}+1,y_{0})}$ に近いのでその点を選び、逆なら ${\displaystyle (x_{0}+1,y_{0}+1)}$ を選べばよい。この中間点における関数の値のみで選択すべき点が決まる。

右図において、青い点 (2,2) は直線上にあり、緑の (3,2) と (3,3) が次に選択すべき点の候補である。黒い点 (3, 2.5) はその2つの候補点の中間点である。

整数演算の場合

中間点での関数値を求める代わりに、2点における関数値の差を使うことができる。それにより整数のみで計算可能となり、浮動小数点数を使うより一般に高速となる。この代替技法を導出するため、その差を次のように定義する。

${\displaystyle D=f(x_{0}+1,y_{0}+1/2)-f(x_{0},y_{0})}$

始点では ${\displaystyle f(x_{0},y_{0})=0}$ であるため、この式は中間点の関数値を求めることと等価である。この式を変形すると次のようになる。

${\displaystyle {\begin{aligned}D&=\left[A(x_{0}+1)+B(y_{0}+1/2)+C\right]-\left[Ax_{0}+By_{0}+C\right]\\&=A+{\frac {1}{2}}B\end{aligned}}}$

中間点の関数値を求める場合と同様、Dが正なら ${\displaystyle (x_{0}+1,y_{0}+1)}$ を選び、さもなくば ${\displaystyle (x_{0}+1,y_{0})}$ を選ぶ。

さらに2つ目の点の選択は次のようになる。

${\displaystyle f(x_{0}+2,y_{0}+1/2)-f(x_{0}+1,y_{0}+1/2)=A=\Delta y}$

${\displaystyle f(x_{0}+2,y_{0}+3/2)-f(x_{0}+1,y_{0}+1/2)=A+B=\Delta y-\Delta x}$

この差が正なら ${\displaystyle (x_{0}+2,y_{0}+1)}$ を選び、さもなくば ${\displaystyle (x_{0}+2,y_{0})}$ を選ぶ。この選択は誤差の蓄積によって一般化される。

以上でアルゴリズムの導出が完了した。性能上問題となるのは、Dの初期値で1/2という係数を使っている点である。ここで必要なのは累積差分の正負の符号だけなので、全てを2倍にしても結果には影響しない。

その結果、次のように整数のみでこのアルゴリズムを実装できる。

plot(x0,y0, x1,y1)
  dx=x1-x0
  dy=y1-y0

  D = 2*dy - dx
  plot(x0,y0)
  y=y0

  for x from x0+1 to x1
    if D > 0
      y = y+1
      plot(x,y)
      D = D + (2*dy-2*dx)
    else
      plot(x,y)
      D = D + (2*dy)

${\displaystyle f(x,y)=x-2y+2}$ で表される直線の (0,1) から (6,4) までをこのアルゴリズムで計算した場合の経過を以下に示す。dx=6、dy=3 である。

• D=2*3-6=0
• plot(0,1)
• 1から6までループ
  • x=1: D≤0: plot(1,1), D=6
  • x=2: D>0: y=2, plot(2,2), D=6+(6-12)=0
  • x=3: D≤0: plot(3,2), D=6
  • x=4: D>0: y=3, plot(4,3), D=6+(6-12)=0
  • x=5: D≤0: plot(5,3), D=6
  • x=6: D>0: y=4, plot(6,4), D=6+(6-12)=0

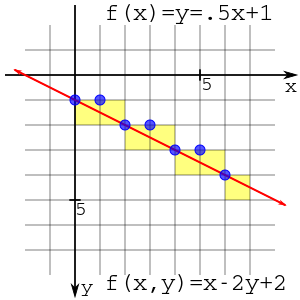
この描画結果を右図に示す。描画は座標上の交点（青い点）またはピクセル（黄色い四角形）で示されている。

全象限について

ここまで述べてきたのは、第一象限かつ、直線の傾きが45度以下の場合（第一八分円）のみについてである。したがって、直交座標系のあらゆる場合を網羅するには全部で8つのケースを考慮する必要がある。

類似のアルゴリズム

ブレゼンハムのアルゴリズムは、DDA（英語版）を若干修正したものと見ることができる（DDAはオーバーラップしない多角形、すなわちポリゴンのラスタライズで使われる）。

除算の代わりに増分誤差を使う原理は、グラフィックスにおいて他にも応用されている。例えば、テクスチャマッピングでのU,V座標(en:UV mapping)計算に使うことができる。また、ゲームでの3次元地形描画でもこの原理が使われることがある。

IBMの Alan Murphy はこのアルゴリズムを拡張した太い直線の描画アルゴリズムを開発した。

脚注

参考文献

• Bresenham, J. E. (1 January 1965). “Algorithm for computer control of a digital plotter”. IBM Systems Journal 4 (1): 25–30. doi:10.1147/sj.41.0025. http://ieeexplore.ieee.org/xpl/tocresult.jsp?isnumber=5388471&punumber=5288519. 
• "The Bresenham Line-Drawing Algorithm", by Colin Flanagan
• Abrash, Michael (1997). Michael Abrash's graphics programming black book. Albany, NY: Coriolis. pp. 654–678. ISBN 978-1-57610-174-2 

関連文献

• Patrick-Gilles Maillot's Thesis MICAD '87 proceedings on CAD/CAM and Computer Graphics, page 591 - ISBN 2-86601-084-1. ブレゼンハムのアルゴリズムを応用して3次元グラフィックスで隠れて見えない直線を削除する技法を示したもの
• Line Thickening by Modification To Bresenham's Algorithm, A.S. Murphy, IBM Technical Disclosure Bulletin, Vol. 20, No. 12, May 1978. ブレゼンハムのアルゴリズムを拡張して太い線を描画する技法を示したもの

外部リンク

• Didactical Javascript implementation（ポルトガル語）
• National Institute of Standards and Technology page on Bresenham's algorithm
• Calcomp 563 Incremental Plotter Information
• 3D extension
• Bresenham 2D, 3D up to 6D
• Bresenham Algorithm in several programming languages
• The Beauty of Bresenham's Algorithm – 直線、円、楕円、ベジェ曲線をプロットする単純な実装例