Automa a stati finiti deterministico

Nella teoria del calcolo, un automa a stati finiti deterministico (ASFD) o deterministic finite automaton (DFA) è un automa a stati finiti dove per ogni coppia di stato e simbolo in ingresso c'è una ed una sola transizione allo stato successivo.

Definizione formale

Un ASFD è una quintupla ${\displaystyle {\mathcal {A}}=\left\langle \Sigma ,S,\delta ,s_{0},F\right\rangle }$ con:

• ${\displaystyle \Sigma =\{a_{0},a_{1},\ldots ,a_{n}\}}$ insieme finito di simboli chiamato alfabeto
• ${\displaystyle S=\{s_{0},s_{1},\ldots ,s_{m}\}}$ insieme finito di stati
• ${\displaystyle \delta :S\times \Sigma \to S}$ funzione di transizione fra stati
• ${\displaystyle s_{0}\in S}$ stato iniziale
• ${\displaystyle F\subseteq S}$ insieme di stati finali o terminali

Dato un ASFD ${\displaystyle {\mathcal {A}}=\left\langle \Sigma ,S,\delta ,s_{0},F\right\rangle }$, una configurazione di ${\displaystyle {\mathcal {A}}}$ è una coppia ${\displaystyle (s,x)}$, dove ${\displaystyle s}$ è uno stato e ${\displaystyle x}$ una stringa dell'alfabeto.

Una configurazione ${\displaystyle (s,x)}$ è detta:

• iniziale se s è lo stato iniziale, ${\displaystyle s=s_{0}}$;
• finale se la stringa in input è vuota, ${\displaystyle x=\varepsilon }$;
• accettante se la stringa in input è vuota e l'automa si trova in uno stato finale, ${\displaystyle x=\varepsilon }$ e ${\displaystyle s\in F}$.

La funzione di transizione induce una relazione di transizione ${\displaystyle \vdash }$ tra due configurazioni, che associa ad una configurazione dell'automa la configurazione successiva.

Dato un ASFD ${\displaystyle {\mathcal {A}}=\left\langle \Sigma ,S,\delta ,s_{0},F\right\rangle }$ e due configurazioni ${\displaystyle (s,x)}$ e ${\displaystyle (s',y)}$ di ${\displaystyle {\mathcal {A}}}$, avremo tra loro una relazione di transizione ${\displaystyle (s,x)\vdash _{\mathcal {A}}(s',y)}$ se valgono:

• esiste un simbolo ${\displaystyle a\in \Sigma }$ tale che ${\displaystyle x=ay}$
• ${\displaystyle \delta (s,a)=s'}$

Una stringa ${\displaystyle x\in \Sigma ^{*}}$ è accettata dall'ASFD ${\displaystyle {\mathcal {A}}}$ se, partendo dalla configurazione iniziale con la stringa ed applicando iterativamente le relazioni di transizione, si perviene ad una configurazione accettante. L'insieme delle stringhe accettate dall'automa forma un linguaggio formale chiamato linguaggio riconosciuto dall'automa. Possiamo quindi dire che ${\displaystyle L({\mathcal {A}})=\{x\in \Sigma ^{*}|(s_{0},x)\vdash _{\mathcal {A}}^{*}(s,\varepsilon ),s\in F\}}$, ovvero che il linguaggio riconosciuto dall'ASFD è composto da tutte le stringhe sull'alfabeto dato per cui l'automa termina in uno stato finale.

Il teorema di Kleene dimostra che la collezione dei linguaggi riconosciuti da automi a stati finiti deterministici coincide sia con la collezione dei linguaggi regolari che con i linguaggi definiti da espressioni regolari.

Le espressioni regolari sono chiamate anche espressioni razionali e di conseguenza i linguaggi che esse forniscono sono detti linguaggi razionali; questi termini sono giustificati dal fatto che questi oggetti si possono studiare con metodi algebrici, più precisamente mediante semigruppi finiti.^{[senza fonte]}

Funzione delta estesa

Un modo alternativo per descrivere il comportamento dell'automa è quello di definire la funzione di transizione estesa che estende la funzione di transizione dai simboli alle stringhe. Indichiamo la nuova funzione come ${\displaystyle {\bar {\delta }}:(S\times \Sigma ^{*})\to S}$.

La sua definizione viene data induttivamente sulla lunghezza della stringa.

• Base: ${\displaystyle {\bar {\delta }}(q,\varepsilon )=q}$.
• Ipotesi induttiva: ${\displaystyle {\bar {\delta }}(q,x)=p}$.
• Passo induttivo: ${\displaystyle {\bar {\delta }}(q,\omega )={\delta }({\bar {\delta }}(q,x),a)={\delta }(p,a)=r}$, con ${\displaystyle \omega =xa}$ (dove ${\displaystyle a\in \Sigma }$ e ${\displaystyle x\in \Sigma ^{*}}$).

Sfruttando la funzione delta estesa è possibile ridefinire il linguaggio accettato dall'automa come:

${\displaystyle L({\mathcal {A}})=\{x\in \Sigma ^{*}|{\bar {\delta }}(s_{0},x)\in F\}}$

Esempio

Il seguente esempio è una ASFD ${\displaystyle {\mathcal {A}}}$, con un alfabeto binario, che determina se l'input contiene un numero pari di zeri.

${\displaystyle {\mathcal {A}}=\left\langle \Sigma ,S,\delta ,s_{0},F\right\rangle }$ con:

• ${\displaystyle \Sigma =\{0,1\}}$ alfabeto binario
• ${\displaystyle S=\{S_{1},S_{2}\}}$ stati
• ${\displaystyle s_{0}=S_{1}}$ stato iniziale
• ${\displaystyle F=\{S_{1}\}}$ stati finali

• ${\displaystyle \delta =\left\{{\begin{matrix}\delta (S_{1},0)=S_{2}\\\delta (S_{1},1)=S_{1}\\\delta (S_{2},0)=S_{1}\\\delta (S_{2},1)=S_{2}\end{matrix}}\right.}$

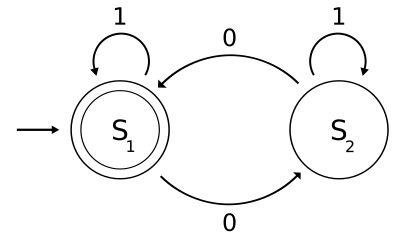
La tabella di transizione è la seguente:

	0	1
S1	S2	S1
S2	S1	S2

Semplicemente, lo stato ${\displaystyle S_{1}}$ rappresenta lo stato in cui abbiamo sempre un numero pari di zeri nell'input, mentre ${\displaystyle S_{2}}$ indica un numero dispari di zeri. Un 1 in input non cambia lo stato dell'automa. Quando l'input termina, lo stato mostrerà se l'input conteneva un numero pari di zeri, o no.

Da questo ASFD possiamo ricavare la grammatica regolare che genera il linguaggio regolare riconosciuto dall'ASFD:

${\displaystyle S_{1}\to 0S_{2}\;|\;1S_{1}\;|\;1\;|\;\varepsilon }$

${\displaystyle S_{2}\to 0S_{1}\;|\;1S_{2}\;|\;0}$

Il linguaggio riconosciuto da ${\displaystyle {\mathcal {A}}}$ può essere descritto dal linguaggio regolare dato dalla seguente espressione regolare:

${\displaystyle 1^{*}(01^{*}01^{*})^{*}}$

Bibliografia

• Giorgio Ausiello, Fabrizio d'Amore; Giorgio Gambosi, Linguaggi, Modelli, Complessità, Franco Angeli Editore, 2003, ISBN 88-464-4470-1.
• (EN) finite state machine (FSM), in Hargrave's Communications Dictionary, Hoboken, Wiley, 2001.
• (EN) Sequential machine, in Encyclopedia of Computer Science, Hoboken, Wiley, 2003.
• (EN) John E. Hopcroft, Rajeev Motwani; Jeffrey D. Ullman, Finite Automata, in Introduction to Automata Theory, Languages, and Computation, Addison Wesley, 15 luglio 2006, ISBN 978-0-321-46225-1.
• (EN) Martin Davis, Ron Sigal; Elaine J. Weyuker, Finite Automata, in Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science, Morgan Kaufmann, 17 febbraio 1994, ISBN 978-0-12-206382-4.

Voci correlate

• Automa a stati finiti non deterministico
• Automa a stati finiti
• Macchina di Moore
• Macchina di Mealy
• Linguaggio regolare
• Grammatica regolare
• Espressione regolare
• Minimizzazione di DFA

Portale Informatica: accedi alle voci di Wikipedia che trattano di Informatica