Inégalité de Bonnesen

En mathématiques, l'inégalité de Bonnesen^[1],[2] est un raffinement de l'inégalité isopérimétrique dans le plan euclidien. Elle énonce qu'une surface S d'aire A et de longueur L vérifie l'inégalité

${\displaystyle \pi ^{2}(R-r)^{2}\leq L^{2}-4\pi A}$

où r et R sont respectivement les rayons du cercle inscrit^[3] et du cercle circonscrit^[4] à cette surface S.

L'inégalité de Bonnesen généralise l'inégalité isopérimétrique car elle implique cette dernière. En effet, d'après l'inégalité de Bonnesen,

${\displaystyle 4\pi A\leq L^{2}-\underbrace {\pi ^{2}(R-r)^{2}} _{\geq 0}\leq L^{2}}$

car R ≥ r. On retrouve bien l'inégalité isopérimétrique

${\displaystyle L^{2}\geq 4\pi A.}$

L'inégalité de Bonnesen est nommée en l'honneur de Tommy Bonnesen (en) qui fut le premier à établir cette inégalité^[5].

Démonstration

La démonstration présentée ici, due à Hugo Hadwiger^[6], montre un résultat un peu plus précis: les deux rayons r et R sont situés entre les deux racines de la fonction polynomiale du second degré qui à t associe l'aire de la surface S + tB où tB est la boule de rayon t centrée en l'origine.

• La valeur –r est d'image négative par le polynôme qui, à t associe l'aire de la surface S + tB :

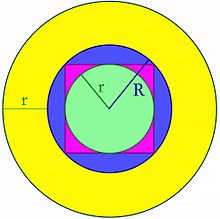
On considère un compact convexe non vide S, un cercle inscrit, de rayon r et un cercle circonscrit C de rayon R. Cette situation est illustrée sur la figure de gauche, le compact convexe est le carré violet, le cercle C est illustré en bleu et le cercle inscrit en vert. La technique utilisée consiste à considérer la zone bleue Z correspondant aux points de C qui ne sont pas dans S. La surface Z + rB est doublement mesurée, les symboles rB désignent ici la boule de rayon r et de centre le vecteur nul. Cette figure recouvre intégralement S et définit un disque de rayon R + r, illustré en jaune. On en déduit une première égalité :

${\displaystyle A(Z+r{\mathcal {B}})=\pi (R+r)^{2}.}$

On découpe alors la surface Z en deux par une droite Δ passant par les centres des deux cercles inscrit et circonscrit. La partie supérieure de Z est notée Z_s, comme indiquée sur l'illustration à droite. La somme de Minkowski de Z_s et de rB correspond, dans la partie supérieure à la droite Δ, à un demi-disque, de rayon R + r. Si l₁ et l₂ sont les longueurs des deux intersections de Z avec Δ (voir la figure), l'intersection de la somme avec la partie inférieure à la droite Δ possède une aire égale à πr² + (l₁ + l₂)r. On en déduit l'égalité :

${\displaystyle A(Z_{s}+r{\mathcal {B}})={\frac {\pi }{2}}(R+r)^{2}+(l_{1}+l_{2})r+\pi r^{2}.}$

Il est aussi possible d'évaluer cette aire à l'aide de la formule de Steiner-Minkowski. Comme Z_s n'est pas convexe, la formule est une majoration et non pas une égalité :

${\displaystyle A(Z_{s}+r{\mathcal {B}})={\frac {\pi }{2}}(R+r)^{2}+(l_{1}+l_{2})r+\pi r^{2}\leq A(Z_{s})+(\pi R+l_{1}+l_{2}+p_{s})r+\pi r^{2}.}$

Ici p_s désigne la longueur de la partie supérieure de la frontière de S. On peut appliquer exactement le même raisonnement à la partie inférieure à la droite Δ. En utilisant l'indice i pour décrire la partie inférieure, on obtient :

${\displaystyle A(Z_{i}+r{\mathcal {B}})={\frac {\pi }{2}}(R+r)^{2}+(l_{1}+l_{2})r+\pi r^{2}\leq A(Z_{i})+(\pi R+l_{1}+l_{2}+p_{i})r+\pi r^{2}.}$

En sommant les deux majorations :

${\displaystyle \pi (R+r)^{2}+2(l_{1}+l_{2})r+2\pi r^{2}\leq A(Z)+2\pi Rr+2\pi r^{2}+2(l_{1}+l_{2})r+pr.}$

Le périmètre p de S est en effet la somme de p_s et de p_i. L'aire de Z est aussi égale à la différence de l'aire d'un disque de rayon R avec l'aire a de S, ce qui donne :

${\displaystyle \pi (R+r)^{2}+2\pi r^{2}\leq \pi R^{2}-a+2\pi Rr+2\pi r^{2}+pr\quad {\text{et}}\quad a-pr+\pi r^{2}\leq 0.}$

La dernière majoration signifie que -r est d'image négative par le polynôme associant à t l'aire de S + tB.

• La valeur –R est d'image négative par le polynôme qui, à t associe l'aire de la surface S + tB :

On applique exactement le même raisonnement que le précédent en remplaçant le coefficient r par R, le rayon du cercle circonscrit (R n'est-il pas trop grand pour que cela soit possible ?). On obtient la majoration :

${\displaystyle \pi (2R)^{2}+2\pi R^{2}\leq \pi R^{2}-a+2\pi R^{2}+2\pi R^{2}+pR\quad {\text{et}}\quad a-pR+\pi R^{2}\leq 0,}$

ce qui démontre la proposition.

• L'inégalité de Bonnesen est vérifiée :

Dire que –r et –R ont une image négative par le polynôme revient à dire que ces valeurs se trouvent entre les racines :

${\displaystyle -{\frac {p+{\sqrt {p^{2}-4\pi a}}}{2\pi }}\leq -R\leq -r\leq -{\frac {p-{\sqrt {p^{2}-4\pi a}}}{2\pi }}.}$

Cela signifie aussi que la distance qui sépare R et r est plus petite que le rapport entre le discriminant et π :

${\displaystyle R-r\leq {\frac {\sqrt {p^{2}-4\pi a}}{\pi }}\quad {\text{et}}\quad p^{2}-4\pi a\geq \pi ^{2}(R-r)^{2}.}$

Références

• Portail de la géométrie