Icosaèdre tronqué

Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (août 2023).

Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes.

Icosaèdre tronqué

Éléments

Faces	Arêtes	Sommets
32 (20 hexagones réguliers et 12 pentagones réguliers)	90	60 de degré 3

Données clés

Type	Solide d'Archimède
Caractéristique	2
Propriétés	Semi-régulier et convexe, zonoèdre
Groupe de symétrie	A5 × C2
Dual	Pentakidodécaèdre

modifier

L'icosaèdre tronqué est un solide d'Archimède. Il comprend 12 faces pentagonales régulières, 20 faces hexagonales régulières, 60 sommets et 90 arêtes.

Construction

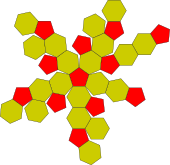
Ce polyèdre peut être construit à partir d'un icosaèdre (solide formé de 20 faces triangulaires régulières) avec une troncature des 12 sommets telle qu'un tiers de chaque arête est enlevé à chaque extrémité. Ceci crée 12 nouvelles faces pentagonales, et remplace les 20 faces triangulaires d'origine par des hexagones réguliers. Ainsi, la longueur des arêtes est un tiers de la longueur des arêtes originales.

Dénomination

Archimède lui avait donné le nom de triacontadoèdre. Mais ce nom de triacontadoèdre, qui désigne un polyèdre semi-régulier à 32 faces, est ambigu : il existe en effet trois polyèdres semi-réguliers à 32 faces.^{[réf. nécessaire]}

Coordonnées canoniques

Les coordonnées canoniques pour les sommets d'un icosaèdre tronqué centré à l'origine sont respectivement les rectangles orthogonaux, les pavés orthogonaux, puis le long des pavés orthogonaux :

${\displaystyle \left(0,\pm 1,\pm 3\varphi \right),\left(\pm 1,\pm 3\varphi ,0\right),\left(\pm 3\varphi ,0,\pm 1\right)}$

${\displaystyle \left(\pm 2,\pm (1+2\varphi ),\pm \varphi \right),\left(\pm (1+2\varphi ),\pm \varphi ,\pm 2\right),\left(\pm \varphi ,\pm 2,\pm (1+2\varphi )\right)}$

${\displaystyle \left(\pm 1,\pm (2+\varphi ),\pm 2\varphi \right),\left(\pm (2+\varphi ),\pm 2\varphi ,\pm 1\right),\left(\pm 2\varphi ,\pm 1,\pm (2+\varphi )\right)}$

où ${\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}$ est le nombre d'or. En utilisant ${\displaystyle \varphi ^{2}=\varphi +1}$, on vérifie que tous ces sommets sont sur une sphère de rayon ${\displaystyle {\sqrt {9\varphi +10}}}$, centrée à l'origine et les arêtes ont une longueur 2.

Relations géométriques

L'icosaèdre tronqué vérifie facilement la caractéristique d'Euler :

32 + 60 − 90 = 2.

Avec des arêtes égales à l'unité, la surface est (arrondie) de 21 pour les pentagones et 52 pour les hexagones, faisant 73 en tout (voir aires des polygones réguliers).

Applications

Un ballon de football comprend le même motif de pentagones réguliers et d'hexagones réguliers, mais est plus sphérique en raison de la pression du gonflage et de l'élasticité de la matière avec laquelle on fabrique la balle.

Cette forme fut aussi la configuration des lentilles utilisées pour concentrer les ondes de choc d'explosion des détonateurs dans les bombes atomiques Gadget et Fat Man^[1].

L'icosaèdre tronqué est aussi utilisé comme un modèle de la molécule de buckminsterfullerène (C₆₀). Les diamètres du ballon de football et de la molécule de buckminsterfullerène sont respectivement de 22 cm et d'environ 1 nm, par conséquent, le rapport de taille est de 200 000 000 pour 1.

L'icosaèdre tronqué dans les arts

Un icosaèdre tronqué avec des « arêtes solides » est un dessin de Léonard de Vinci, illustrant le livre De divina proportione de Luca Pacioli^[2].

Notes et références

Voir aussi

Articles connexes

• Ballon de football hyperbolique (en)
• Dodécaèdre
• Dodécaèdre tronqué
• Fullerène
• Icosidodécaèdre
• Polyèdre uniforme
• Triacontaèdre rhombique tronqué

Liens externes

• « Icosaèdre tronqué », sur Mathcurve
• (en) Eric W. Weisstein, « Truncated Icosahedron », sur MathWorld
• (en) Patron en papier d'un icosaèdre tronqué
• (en) Icosaèdre tronqué bondissant Réalité virtuelle (JVM nécessaire)

Bibliographie

(en) Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979 (ISBN 0-486-23729-X)

• Portail de la géométrie