Minkowski functional

Function made from a set

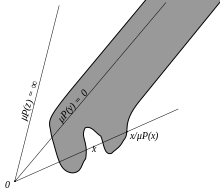
In mathematics, in the field of functional analysis, a Minkowski functional (after Hermann Minkowski) or gauge function is a function that recovers a notion of distance on a linear space.

If K {\displaystyle K} is a subset of a real or complex vector space X , {\displaystyle X,} then the Minkowski functional or gauge of K {\displaystyle K} is defined to be the function p K : X → [ 0 , ∞ ] , {\displaystyle p_{K}:X\to [0,\infty ],} valued in the extended real numbers, defined by

p K ( x ) := inf { r ∈ R : r > 0  and  x ∈ r K }  for every  x ∈ X , {\displaystyle p_{K}(x):=\inf\{r\in \mathbb {R} :r>0{\text{ and }}x\in rK\}\quad {\text{ for every }}x\in X,}
where the infimum of the empty set is defined to be positive infinity ∞ {\displaystyle \,\infty \,} (which is not a real number so that p K ( x ) {\displaystyle p_{K}(x)} would then not be real-valued).

The set K {\displaystyle K} is often assumed/picked to have properties, such as being an absorbing disk in X , {\displaystyle X,} that guarantee that p K {\displaystyle p_{K}} will be a real-valued seminorm on X . {\displaystyle X.} In fact, every seminorm p {\displaystyle p} on X {\displaystyle X} is equal to the Minkowski functional (that is, p = p K {\displaystyle p=p_{K}} ) of any subset K {\displaystyle K} of X {\displaystyle X} satisfying { x ∈ X : p ( x ) < 1 } ⊆ K ⊆ { x ∈ X : p ( x ) ≤ 1 } {\displaystyle \{x\in X:p(x)<1\}\subseteq K\subseteq \{x\in X:p(x)\leq 1\}} (where all three of these sets are necessarily absorbing in X {\displaystyle X} and the first and last are also disks).

Thus every seminorm (which is a function defined by purely algebraic properties) can be associated (non-uniquely) with an absorbing disk (which is a set with certain geometric properties) and conversely, every absorbing disk can be associated with its Minkowski functional (which will necessarily be a seminorm). These relationships between seminorms, Minkowski functionals, and absorbing disks is a major reason why Minkowski functionals are studied and used in functional analysis. In particular, through these relationships, Minkowski functionals allow one to "translate" certain geometric properties of a subset of X {\displaystyle X} into certain algebraic properties of a function on X . {\displaystyle X.}

The Minkowski function is always non-negative (meaning p K ≥ 0 {\displaystyle p_{K}\geq 0} ). This property of being nonnegative stands in contrast to other classes of functions, such as sublinear functions and real linear functionals, that do allow negative values. However, p K {\displaystyle p_{K}} might not be real-valued since for any given x ∈ X , {\displaystyle x\in X,} the value p K ( x ) {\displaystyle p_{K}(x)} is a real number if and only if { r > 0 : x ∈ r K } {\displaystyle \{r>0:x\in rK\}} is not empty. Consequently, K {\displaystyle K} is usually assumed to have properties (such as being absorbing in X , {\displaystyle X,} for instance) that will guarantee that p K {\displaystyle p_{K}} is real-valued.

Definition

Let K {\displaystyle K} be a subset of a real or complex vector space X . {\displaystyle X.} Define the gauge of K {\displaystyle K} or the Minkowski functional associated with or induced by K {\displaystyle K} as being the function p K : X → [ 0 , ∞ ] , {\displaystyle p_{K}:X\to [0,\infty ],} valued in the extended real numbers, defined by

p K ( x ) := inf { r > 0 : x ∈ r K } , {\displaystyle p_{K}(x):=\inf\{r>0:x\in rK\},}
where recall that the infimum of the empty set is ∞ {\displaystyle \,\infty \,} (that is, inf ∅ = ∞ {\displaystyle \inf \varnothing =\infty } ). Here, { r > 0 : x ∈ r K } {\displaystyle \{r>0:x\in rK\}} is shorthand for { r ∈ R : r > 0  and  x ∈ r K } . {\displaystyle \{r\in \mathbb {R} :r>0{\text{ and }}x\in rK\}.}

For any x ∈ X , {\displaystyle x\in X,} p K ( x ) ≠ ∞ {\displaystyle p_{K}(x)\neq \infty } if and only if { r > 0 : x ∈ r K } {\displaystyle \{r>0:x\in rK\}} is not empty. The arithmetic operations on R {\displaystyle \mathbb {R} } can be extended to operate on ± ∞ , {\displaystyle \pm \infty ,} where r ± ∞ := 0 {\displaystyle {\frac {r}{\pm \infty }}:=0} for all non-zero real − ∞ < r < ∞ . {\displaystyle -\infty <r<\infty .} The products 0 ⋅ ∞ {\displaystyle 0\cdot \infty } and 0 ⋅ − ∞ {\displaystyle 0\cdot -\infty } remain undefined.

Some conditions making a gauge real-valued

In the field of convex analysis, the map p K {\displaystyle p_{K}} taking on the value of ∞ {\displaystyle \,\infty \,} is not necessarily an issue. However, in functional analysis p K {\displaystyle p_{K}} is almost always real-valued (that is, to never take on the value of ∞ {\displaystyle \,\infty \,} ), which happens if and only if the set { r > 0 : x ∈ r K } {\displaystyle \{r>0:x\in rK\}} is non-empty for every x ∈ X . {\displaystyle x\in X.}

In order for p K {\displaystyle p_{K}} to be real-valued, it suffices for the origin of X {\displaystyle X} to belong to the algebraic interior or core of K {\displaystyle K} in X . {\displaystyle X.} [1] If K {\displaystyle K} is absorbing in X , {\displaystyle X,} where recall that this implies that 0 ∈ K , {\displaystyle 0\in K,} then the origin belongs to the algebraic interior of K {\displaystyle K} in X {\displaystyle X} and thus p K {\displaystyle p_{K}} is real-valued. Characterizations of when p K {\displaystyle p_{K}} is real-valued are given below.

Motivating examples

Example 1

Consider a normed vector space ( X , ‖ ⋅ ‖ ) , {\displaystyle (X,\|\,\cdot \,\|),} with the norm ‖ ⋅ ‖ {\displaystyle \|\,\cdot \,\|} and let U := { x ∈ X : ‖ x ‖ ≤ 1 } {\displaystyle U:=\{x\in X:\|x\|\leq 1\}} be the unit ball in X . {\displaystyle X.} Then for every x ∈ X , {\displaystyle x\in X,} ‖ x ‖ = p U ( x ) . {\displaystyle \|x\|=p_{U}(x).} Thus the Minkowski functional p U {\displaystyle p_{U}} is just the norm on X . {\displaystyle X.}

Example 2

Let X {\displaystyle X} be a vector space without topology with underlying scalar field K . {\displaystyle \mathbb {K} .} Let f : X → K {\displaystyle f:X\to \mathbb {K} } be any linear functional on X {\displaystyle X} (not necessarily continuous). Fix a > 0. {\displaystyle a>0.} Let K {\displaystyle K} be the set

K := { x ∈ X : | f ( x ) | ≤ a } {\displaystyle K:=\{x\in X:|f(x)|\leq a\}}
and let p K {\displaystyle p_{K}} be the Minkowski functional of K . {\displaystyle K.} Then
p K ( x ) = 1 a | f ( x ) |  for all  x ∈ X . {\displaystyle p_{K}(x)={\frac {1}{a}}|f(x)|\quad {\text{ for all }}x\in X.}
The function p K {\displaystyle p_{K}} has the following properties:

  1. It is subadditive: p K ( x + y ) ≤ p K ( x ) + p K ( y ) . {\displaystyle p_{K}(x+y)\leq p_{K}(x)+p_{K}(y).}
  2. It is absolutely homogeneous: p K ( s x ) = | s | p K ( x ) {\displaystyle p_{K}(sx)=|s|p_{K}(x)} for all scalars s . {\displaystyle s.}
  3. It is nonnegative: p K ≥ 0. {\displaystyle p_{K}\geq 0.}

Therefore, p K {\displaystyle p_{K}} is a seminorm on X , {\displaystyle X,} with an induced topology. This is characteristic of Minkowski functionals defined via "nice" sets. There is a one-to-one correspondence between seminorms and the Minkowski functional given by such sets. What is meant precisely by "nice" is discussed in the section below.

Notice that, in contrast to a stronger requirement for a norm, p K ( x ) = 0 {\displaystyle p_{K}(x)=0} need not imply x = 0. {\displaystyle x=0.} In the above example, one can take a nonzero x {\displaystyle x} from the kernel of f . {\displaystyle f.} Consequently, the resulting topology need not be Hausdorff.

Common conditions guaranteeing gauges are seminorms

To guarantee that p K ( 0 ) = 0 , {\displaystyle p_{K}(0)=0,} it will henceforth be assumed that 0 ∈ K . {\displaystyle 0\in K.}

In order for p K {\displaystyle p_{K}} to be a seminorm, it suffices for K {\displaystyle K} to be a disk (that is, convex and balanced) and absorbing in X , {\displaystyle X,} which are the most common assumption placed on K . {\displaystyle K.}

Theorem[2] — If K {\displaystyle K} is an absorbing disk in a vector space X {\displaystyle X} then the Minkowski functional of K , {\displaystyle K,} which is the map p K : X → [ 0 , ∞ ) {\displaystyle p_{K}:X\to [0,\infty )} defined by

p K ( x ) := inf { r > 0 : x ∈ r K } , {\displaystyle p_{K}(x):=\inf\{r>0:x\in rK\},}
is a seminorm on X . {\displaystyle X.} Moreover,
p K ( x ) = 1 sup { r > 0 : r x ∈ K } . {\displaystyle p_{K}(x)={\frac {1}{\sup\{r>0:rx\in K\}}}.}

More generally, if K {\displaystyle K} is convex and the origin belongs to the algebraic interior of K , {\displaystyle K,} then p K {\displaystyle p_{K}} is a nonnegative sublinear functional on X , {\displaystyle X,} which implies in particular that it is subadditive and positive homogeneous. If K {\displaystyle K} is absorbing in X {\displaystyle X} then p [ 0 , 1 ] K {\displaystyle p_{[0,1]K}} is positive homogeneous, meaning that p [ 0 , 1 ] K ( s x ) = s p [ 0 , 1 ] K ( x ) {\displaystyle p_{[0,1]K}(sx)=sp_{[0,1]K}(x)} for all real s ≥ 0 , {\displaystyle s\geq 0,} where [ 0 , 1 ] K = { t k : t ∈ [ 0 , 1 ] , k ∈ K } . {\displaystyle [0,1]K=\{tk:t\in [0,1],k\in K\}.} [3] If q {\displaystyle q} is a nonnegative real-valued function on X {\displaystyle X} that is positive homogeneous, then the sets U := { x ∈ X : q ( x ) < 1 } {\displaystyle U:=\{x\in X:q(x)<1\}} and D := { x ∈ X : q ( x ) ≤ 1 } {\displaystyle D:=\{x\in X:q(x)\leq 1\}} satisfy [ 0 , 1 ] U = U {\displaystyle [0,1]U=U} and [ 0 , 1 ] D = D ; {\displaystyle [0,1]D=D;} if in addition q {\displaystyle q} is absolutely homogeneous then both U {\displaystyle U} and D {\displaystyle D} are balanced.[3]

Gauges of absorbing disks

Arguably the most common requirements placed on a set K {\displaystyle K} to guarantee that p K {\displaystyle p_{K}} is a seminorm are that K {\displaystyle K} be an absorbing disk in X . {\displaystyle X.} Due to how common these assumptions are, the properties of a Minkowski functional p K {\displaystyle p_{K}} when K {\displaystyle K} is an absorbing disk will now be investigated. Since all of the results mentioned above made few (if any) assumptions on K , {\displaystyle K,} they can be applied in this special case.

Theorem — Assume that K {\displaystyle K} is an absorbing subset of X . {\displaystyle X.} It is shown that:

  1. If K {\displaystyle K} is convex then p K {\displaystyle p_{K}} is subadditive.
  2. If K {\displaystyle K} is balanced then p K {\displaystyle p_{K}} is absolutely homogeneous; that is, p K ( s x ) = | s | p K ( x ) {\displaystyle p_{K}(sx)=|s|p_{K}(x)} for all scalars s . {\displaystyle s.}
Proof that the Gauge of an absorbing disk is a seminorm

Convexity and subadditivity

A simple geometric argument that shows convexity of K {\displaystyle K} implies subadditivity is as follows. Suppose for the moment that p K ( x ) = p K ( y ) = r . {\displaystyle p_{K}(x)=p_{K}(y)=r.} Then for all e > 0 , {\displaystyle e>0,} x , y ∈ K e := ( r , e ) K . {\displaystyle x,y\in K_{e}:=(r,e)K.} Since K {\displaystyle K} is convex and r + e ≠ 0 , {\displaystyle r+e\neq 0,} K e {\displaystyle K_{e}} is also convex. Therefore, 1 2 x + 1 2 y ∈ K e . {\displaystyle {\frac {1}{2}}x+{\frac {1}{2}}y\in K_{e}.} By definition of the Minkowski functional p K , {\displaystyle p_{K},}

p K ( 1 2 x + 1 2 y ) ≤ r + e = 1 2 p K ( x ) + 1 2 p K ( y ) + e . {\displaystyle p_{K}\left({\frac {1}{2}}x+{\frac {1}{2}}y\right)\leq r+e={\frac {1}{2}}p_{K}(x)+{\frac {1}{2}}p_{K}(y)+e.}

But the left hand side is 1 2 p K ( x + y ) , {\displaystyle {\frac {1}{2}}p_{K}(x+y),} so that

p K ( x + y ) ≤ p K ( x ) + p K ( y ) + 2 e . {\displaystyle p_{K}(x+y)\leq p_{K}(x)+p_{K}(y)+2e.}

Since e > 0 {\displaystyle e>0} was arbitrary, it follows that p K ( x + y ) ≤ p K ( x ) + p K ( y ) , {\displaystyle p_{K}(x+y)\leq p_{K}(x)+p_{K}(y),} which is the desired inequality. The general case p K ( x ) > p K ( y ) {\displaystyle p_{K}(x)>p_{K}(y)} is obtained after the obvious modification.

Convexity of K , {\displaystyle K,} together with the initial assumption that the set { r > 0 : x ∈ r K } {\displaystyle \{r>0:x\in rK\}} is nonempty, implies that K {\displaystyle K} is absorbing.

Balancedness and absolute homogeneity

Notice that K {\displaystyle K} being balanced implies that

λ x ∈ r K if and only if x ∈ r | λ | K . {\displaystyle \lambda x\in rK\quad {\mbox{if and only if}}\quad x\in {\frac {r}{|\lambda |}}K.}

Therefore

p K ( λ x ) = inf { r > 0 : λ x ∈ r K } = inf { r > 0 : x ∈ r | λ | K } = inf { | λ | r | λ | > 0 : x ∈ r | λ | K } = | λ | p K ( x ) . {\displaystyle p_{K}(\lambda x)=\inf \left\{r>0:\lambda x\in rK\right\}=\inf \left\{r>0:x\in {\frac {r}{|\lambda |}}K\right\}=\inf \left\{|\lambda |{\frac {r}{|\lambda |}}>0:x\in {\frac {r}{|\lambda |}}K\right\}=|\lambda |p_{K}(x).}

Algebraic properties

Let X {\displaystyle X} be a real or complex vector space and let K {\displaystyle K} be an absorbing disk in X . {\displaystyle X.}

  • p K {\displaystyle p_{K}} is a seminorm on X . {\displaystyle X.}
  • p K {\displaystyle p_{K}} is a norm on X {\displaystyle X} if and only if K {\displaystyle K} does not contain a non-trivial vector subspace.[4]
  • p s K = 1 | s | p K {\displaystyle p_{sK}={\frac {1}{|s|}}p_{K}} for any scalar s ≠ 0. {\displaystyle s\neq 0.} [4]
  • If J {\displaystyle J} is an absorbing disk in X {\displaystyle X} and J ⊆ K {\displaystyle J\subseteq K} then p K ≤ p J . {\displaystyle p_{K}\leq p_{J}.}
  • If K {\displaystyle K} is a set satisfying { x ∈ X : p ( x ) < 1 } ⊆ K ⊆ { x ∈ X : p ( x ) ≤ 1 } {\displaystyle \{x\in X:p(x)<1\}\;\subseteq \;K\;\subseteq \;\{x\in X:p(x)\leq 1\}} then K {\displaystyle K} is absorbing in X {\displaystyle X} and p = p K , {\displaystyle p=p_{K},} where p K {\displaystyle p_{K}} is the Minkowski functional associated with K ; {\displaystyle K;} that is, it is the gauge of K . {\displaystyle K.} [5]
    • In particular, if K {\displaystyle K} is as above and q {\displaystyle q} is any seminorm on X , {\displaystyle X,} then q = p {\displaystyle q=p} if and only if { x ∈ X : q ( x ) < 1 } ⊆ K ⊆ { x ∈ X : q ( x ) ≤ 1 } . {\displaystyle \{x\in X:q(x)<1\}\;\subseteq \;K\;\subseteq \;\{x\in X:q(x)\leq 1\}.} [5]
  • If x ∈ X {\displaystyle x\in X} satisfies p K ( x ) < 1 {\displaystyle p_{K}(x)<1} then x ∈ K . {\displaystyle x\in K.}

Topological properties

Assume that X {\displaystyle X} is a (real or complex) topological vector space (TVS) (not necessarily Hausdorff or locally convex) and let K {\displaystyle K} be an absorbing disk in X . {\displaystyle X.} Then

Int X ⁡ K ⊆ { x ∈ X : p K ( x ) < 1 } ⊆ K ⊆ { x ∈ X : p K ( x ) ≤ 1 } ⊆ Cl X ⁡ K , {\displaystyle \operatorname {Int} _{X}K\;\subseteq \;\{x\in X:p_{K}(x)<1\}\;\subseteq \;K\;\subseteq \;\{x\in X:p_{K}(x)\leq 1\}\;\subseteq \;\operatorname {Cl} _{X}K,}
where Int X ⁡ K {\displaystyle \operatorname {Int} _{X}K} is the topological interior and Cl X ⁡ K {\displaystyle \operatorname {Cl} _{X}K} is the topological closure of K {\displaystyle K} in X . {\displaystyle X.} [6] Importantly, it was not assumed that p K {\displaystyle p_{K}} was continuous nor was it assumed that K {\displaystyle K} had any topological properties.

Moreover, the Minkowski functional p K {\displaystyle p_{K}} is continuous if and only if K {\displaystyle K} is a neighborhood of the origin in X . {\displaystyle X.} [6] If p K {\displaystyle p_{K}} is continuous then[6]

Int X ⁡ K = { x ∈ X : p K ( x ) < 1 }  and  Cl X ⁡ K = { x ∈ X : p K ( x ) ≤ 1 } . {\displaystyle \operatorname {Int} _{X}K=\{x\in X:p_{K}(x)<1\}\quad {\text{ and }}\quad \operatorname {Cl} _{X}K=\{x\in X:p_{K}(x)\leq 1\}.}

Minimal requirements on the set

This section will investigate the most general case of the gauge of any subset K {\displaystyle K} of X . {\displaystyle X.} The more common special case where K {\displaystyle K} is assumed to be an absorbing disk in X {\displaystyle X} was discussed above.

Properties

All results in this section may be applied to the case where K {\displaystyle K} is an absorbing disk.

Throughout, K {\displaystyle K} is any subset of X . {\displaystyle X.}

Summary — Suppose that K {\displaystyle K} is a subset of a real or complex vector space X . {\displaystyle X.}

  1. Strict positive homogeneity: p K ( r x ) = r p K ( x ) {\displaystyle p_{K}(rx)=rp_{K}(x)} for all x ∈ X {\displaystyle x\in X} and all positive real r > 0. {\displaystyle r>0.}
    • Positive/Nonnegative homogeneity: p K {\displaystyle p_{K}} is nonnegative homogeneous if and only if p K {\displaystyle p_{K}} is real-valued.
      • A map p {\displaystyle p} is called nonnegative homogeneous[7] if p ( r x ) = r p ( x ) {\displaystyle p(rx)=rp(x)} for all x ∈ X {\displaystyle x\in X} and all nonnegative real r ≥ 0. {\displaystyle r\geq 0.} Since 0 ⋅ ∞ {\displaystyle 0\cdot \infty } is undefined, a map that takes infinity as a value is not nonnegative homogeneous.
  2. Real-values: ( 0 , ∞ ) K {\displaystyle (0,\infty )K} is the set of all points on which p K {\displaystyle p_{K}} is real valued. So p K {\displaystyle p_{K}} is real-valued if and only if ( 0 , ∞ ) K = X , {\displaystyle (0,\infty )K=X,} in which case 0 ∈ K . {\displaystyle 0\in K.}
    • Value at 0 {\displaystyle 0} : p K ( 0 ) ≠ ∞ {\displaystyle p_{K}(0)\neq \infty } if and only if 0 ∈ K {\displaystyle 0\in K} if and only if p K ( 0 ) = 0. {\displaystyle p_{K}(0)=0.}
    • Null space: If x ∈ X {\displaystyle x\in X} then p K ( x ) = 0 {\displaystyle p_{K}(x)=0} if and only if ( 0 , ∞ ) x ⊆ ( 0 , 1 ) K {\displaystyle (0,\infty )x\subseteq (0,1)K} if and only if there exists a divergent sequence of positive real numbers t 1 , t 2 , t 3 , ⋯ → ∞ {\displaystyle t_{1},t_{2},t_{3},\cdots \to \infty } such that t n x ∈ K {\displaystyle t_{n}x\in K} for all n . {\displaystyle n.} Moreover, the zero set of p K {\displaystyle p_{K}} is ker ⁡ p K   = def   { y ∈ X : p K ( y ) = 0 } = ⋂ e > 0 ( 0 , e ) K . {\displaystyle \ker p_{K}~{\stackrel {\scriptscriptstyle {\text{def}}}{=}}~\left\{y\in X:p_{K}(y)=0\right\}={\textstyle \bigcap \limits _{e>0}}(0,e)K.}
  3. Comparison to a constant: If 0 ≤ r ≤ ∞ {\displaystyle 0\leq r\leq \infty } then for any x ∈ X , {\displaystyle x\in X,} p K ( x ) < r {\displaystyle p_{K}(x)<r} if and only if x ∈ ( 0 , r ) K ; {\displaystyle x\in (0,r)K;} this can be restated as: If 0 ≤ r ≤ ∞ {\displaystyle 0\leq r\leq \infty } then p K − 1 ( [ 0 , r ) ) = ( 0 , r ) K . {\displaystyle p_{K}^{-1}([0,r))=(0,r)K.}
    • It follows that if 0 ≤ R < ∞ {\displaystyle 0\leq R<\infty } is real then p K − 1 ( [ 0 , R ] ) = ⋂ e > 0 ( 0 , R + e ) K , {\displaystyle p_{K}^{-1}([0,R])={\textstyle \bigcap \limits _{e>0}}(0,R+e)K,} where the set on the right hand side denotes ⋂ e > 0 [ ( 0 , R + e ) K ] {\displaystyle {\textstyle \bigcap \limits _{e>0}}[(0,R+e)K]} and not its subset [ ⋂ e > 0 ( 0 , R + e ) ] K = ( 0 , R ] K . {\displaystyle \left[{\textstyle \bigcap \limits _{e>0}}(0,R+e)\right]K=(0,R]K.} If R > 0 {\displaystyle R>0} then these sets are equal if and only if K {\displaystyle K} contains { y ∈ X : p K ( y ) = 1 } . {\displaystyle \left\{y\in X:p_{K}(y)=1\right\}.}
    • In particular, if x ∈ R K {\displaystyle x\in RK} or x ∈ ( 0 , R ] K {\displaystyle x\in (0,R]K} then p K ( x ) ≤ R , {\displaystyle p_{K}(x)\leq R,} but importantly, the converse is not necessarily true.
  4. Gauge comparison: For any subset L ⊆ X , {\displaystyle L\subseteq X,} p K ≤ p L {\displaystyle p_{K}\leq p_{L}} if and only if ( 0 , 1 ) L ⊆ ( 0 , 1 ) K ; {\displaystyle (0,1)L\subseteq (0,1)K;} thus p L = p K {\displaystyle p_{L}=p_{K}} if and only if ( 0 , 1 ) L = ( 0 , 1 ) K . {\displaystyle (0,1)L=(0,1)K.}
    • The assignment L ↦ p L {\displaystyle L\mapsto p_{L}} is order-reversing in the sense that if K ⊆ L {\displaystyle K\subseteq L} then p L ≤ p K . {\displaystyle p_{L}\leq p_{K}.} [8]
    • Because the set L := ( 0 , 1 ) K {\displaystyle L:=(0,1)K} satisfies ( 0 , 1 ) L = ( 0 , 1 ) K , {\displaystyle (0,1)L=(0,1)K,} it follows that replacing K {\displaystyle K} with p K − 1 ( [ 0 , 1 ) ) = ( 0 , 1 ) K {\displaystyle p_{K}^{-1}([0,1))=(0,1)K} will not change the resulting Minkowski functional. The same is true of L := ( 0 , 1 ] K {\displaystyle L:=(0,1]K} and of L := p K − 1 ( [ 0 , 1 ] ) . {\displaystyle L:=p_{K}^{-1}([0,1]).}
    • If D   = def   { y ∈ X : p K ( y ) = 1  or  p K ( y ) = 0 } {\displaystyle D~{\stackrel {\scriptscriptstyle {\text{def}}}{=}}~\left\{y\in X:p_{K}(y)=1{\text{ or }}p_{K}(y)=0\right\}} then p D = p K {\displaystyle p_{D}=p_{K}} and D {\displaystyle D} has the particularly nice property that if r > 0 {\displaystyle r>0} is real then x ∈ r D {\displaystyle x\in rD} if and only if p D ( x ) = r {\displaystyle p_{D}(x)=r} or p D ( x ) = 0. {\displaystyle p_{D}(x)=0.} [note 1] Moreover, if r > 0 {\displaystyle r>0} is real then p D ( x ) ≤ r {\displaystyle p_{D}(x)\leq r} if and only if x ∈ ( 0 , r ] D . {\displaystyle x\in (0,r]D.}
  5. Subadditive/Triangle inequality: p K {\displaystyle p_{K}} is subadditive if and only if ( 0 , 1 ) K {\displaystyle (0,1)K} is convex. If K {\displaystyle K} is convex then so are both ( 0 , 1 ) K {\displaystyle (0,1)K} and ( 0 , 1 ] K {\displaystyle (0,1]K} and moreover, p K {\displaystyle p_{K}} is subadditive.
  6. Scaling the set: If s ≠ 0 {\displaystyle s\neq 0} is a scalar then p s K ( y ) = p K ( 1 s y ) {\displaystyle p_{sK}(y)=p_{K}\left({\tfrac {1}{s}}y\right)} for all y ∈ X . {\displaystyle y\in X.} Thus if 0 < r < ∞ {\displaystyle 0<r<\infty } is real then p r K ( y ) = p K ( 1 r y ) = 1 r p K ( y ) . {\displaystyle p_{rK}(y)=p_{K}\left({\tfrac {1}{r}}y\right)={\tfrac {1}{r}}p_{K}(y).}
  7. Symmetric: p K {\displaystyle p_{K}} is symmetric (meaning that p K ( − y ) = p K ( y ) {\displaystyle p_{K}(-y)=p_{K}(y)} for all y ∈ X {\displaystyle y\in X} ) if and only if ( 0 , 1 ) K {\displaystyle (0,1)K} is a symmetric set (meaning that ( 0 , 1 ) K = − ( 0 , 1 ) K {\displaystyle (0,1)K=-(0,1)K} ), which happens if and only if p K = p − K . {\displaystyle p_{K}=p_{-K}.}
  8. Absolute homogeneity: p K ( u x ) = p K ( x ) {\displaystyle p_{K}(ux)=p_{K}(x)} for all x ∈ X {\displaystyle x\in X} and all unit length scalars u {\displaystyle u} [note 2] if and only if ( 0 , 1 ) u K ⊆ ( 0 , 1 ) K {\displaystyle (0,1)uK\subseteq (0,1)K} for all unit length scalars u , {\displaystyle u,} in which case p K ( s x ) = | s | p K ( x ) {\displaystyle p_{K}(sx)=|s|p_{K}(x)} for all x ∈ X {\displaystyle x\in X} and all non-zero scalars s ≠ 0. {\displaystyle s\neq 0.} If in addition p K {\displaystyle p_{K}} is also real-valued then this holds for all scalars s {\displaystyle s} (that is, p K {\displaystyle p_{K}} is absolutely homogeneous[note 3]).
    • ( 0 , 1 ) u K ⊆ ( 0 , 1 ) K {\displaystyle (0,1)uK\subseteq (0,1)K} for all unit length u {\displaystyle u} if and only if ( 0 , 1 ) u K = ( 0 , 1 ) K {\displaystyle (0,1)uK=(0,1)K} for all unit length u . {\displaystyle u.}
    • s K ⊆ K {\displaystyle sK\subseteq K} for all unit scalars s {\displaystyle s} if and only if s K = K {\displaystyle sK=K} for all unit scalars s ; {\displaystyle s;} if this is the case then ( 0 , 1 ) K = ( 0 , 1 ) s K {\displaystyle (0,1)K=(0,1)sK} for all unit scalars s . {\displaystyle s.}
    • The Minkowski functional of any balanced set is a balanced function.[8]
  9. Absorbing: If K {\displaystyle K} is convex or balanced and if ( 0 , ∞ ) K = X {\displaystyle (0,\infty )K=X} then K {\displaystyle K} is absorbing in X . {\displaystyle X.}
    • If a set A {\displaystyle A} is absorbing in X {\displaystyle X} and A ⊆ K {\displaystyle A\subseteq K} then K {\displaystyle K} is absorbing in X . {\displaystyle X.}
    • If K {\displaystyle K} is convex and 0 ∈ K {\displaystyle 0\in K} then [ 0 , 1 ] K = K , {\displaystyle [0,1]K=K,} in which case ( 0 , 1 ) K ⊆ K . {\displaystyle (0,1)K\subseteq K.}
  10. Restriction to a vector subspace: If S {\displaystyle S} is a vector subspace of X {\displaystyle X} and if p K ∩ S : S → [ 0 , ∞ ] {\displaystyle p_{K\cap S}:S\to [0,\infty ]} denotes the Minkowski functional of K ∩ S {\displaystyle K\cap S} on S , {\displaystyle S,} then p K | S = p K ∩ S , {\displaystyle p_{K}{\big \vert }_{S}=p_{K\cap S},} where p K | S {\displaystyle p_{K}{\big \vert }_{S}} denotes the restriction of p K {\displaystyle p_{K}} to S . {\displaystyle S.}
Proof

The proofs of these basic properties are straightforward exercises so only the proofs of the most important statements are given.

The proof that a convex subset A ⊆ X {\displaystyle A\subseteq X} that satisfies ( 0 , ∞ ) A = X {\displaystyle (0,\infty )A=X} is necessarily absorbing in X {\displaystyle X} is straightforward and can be found in the article on absorbing sets.

For any real t > 0 , {\displaystyle t>0,}

{ r > 0 : t x ∈ r K } = { t ( r / t ) : x ∈ ( r / t ) K } = t { s > 0 : x ∈ s K } {\displaystyle \{r>0:tx\in rK\}=\{t(r/t):x\in (r/t)K\}=t\{s>0:x\in sK\}}
so that taking the infimum of both sides shows that
p K ( t x ) = inf { r > 0 : t x ∈ r K } = t inf { s > 0 : x ∈ s K } = t p K ( x ) . {\displaystyle p_{K}(tx)=\inf\{r>0:tx\in rK\}=t\inf\{s>0:x\in sK\}=tp_{K}(x).}
This proves that Minkowski functionals are strictly positive homogeneous. For 0 ⋅ p K ( x ) {\displaystyle 0\cdot p_{K}(x)} to be well-defined, it is necessary and sufficient that p K ( x ) ≠ ∞ ; {\displaystyle p_{K}(x)\neq \infty ;} thus p K ( t x ) = t p K ( x ) {\displaystyle p_{K}(tx)=tp_{K}(x)} for all x ∈ X {\displaystyle x\in X} and all non-negative real t ≥ 0 {\displaystyle t\geq 0} if and only if p K {\displaystyle p_{K}} is real-valued.

The hypothesis of statement (7) allows us to conclude that p K ( s x ) = p K ( x ) {\displaystyle p_{K}(sx)=p_{K}(x)} for all x ∈ X {\displaystyle x\in X} and all scalars s {\displaystyle s} satisfying | s | = 1. {\displaystyle |s|=1.} Every scalar s {\displaystyle s} is of the form r e i t {\displaystyle re^{it}} for some real t {\displaystyle t} where r := | s | ≥ 0 {\displaystyle r:=|s|\geq 0} and e i t {\displaystyle e^{it}} is real if and only if s {\displaystyle s} is real. The results in the statement about absolute homogeneity follow immediately from the aforementioned conclusion, from the strict positive homogeneity of p K , {\displaystyle p_{K},} and from the positive homogeneity of p K {\displaystyle p_{K}} when p K {\displaystyle p_{K}} is real-valued. ◼ {\displaystyle \blacksquare }

Examples

  1. If L {\displaystyle {\mathcal {L}}} is a non-empty collection of subsets of X {\displaystyle X} then p ∪ L ( x ) = inf { p L ( x ) : L ∈ L } {\displaystyle p_{\cup {\mathcal {L}}}(x)=\inf \left\{p_{L}(x):L\in {\mathcal {L}}\right\}} for all x ∈ X , {\displaystyle x\in X,} where ∪ L   = def   ⋃ L ∈ L L . {\displaystyle \cup {\mathcal {L}}~{\stackrel {\scriptscriptstyle {\text{def}}}{=}}~{\textstyle \bigcup \limits _{L\in {\mathcal {L}}}}L.}
    • Thus p K ∪ L ( x ) = min { p K ( x ) , p L ( x ) } {\displaystyle p_{K\cup L}(x)=\min \left\{p_{K}(x),p_{L}(x)\right\}} for all x ∈ X . {\displaystyle x\in X.}
  2. If L {\displaystyle {\mathcal {L}}} is a non-empty collection of subsets of X {\displaystyle X} and I ⊆ X {\displaystyle I\subseteq X} satisfies
    { x ∈ X : p L ( x ) < 1  for all  L ∈ L } ⊆ I ⊆ { x ∈ X : p L ( x ) ≤ 1  for all  L ∈ L } {\displaystyle \left\{x\in X:p_{L}(x)<1{\text{ for all }}L\in {\mathcal {L}}\right\}\quad \subseteq \quad I\quad \subseteq \quad \left\{x\in X:p_{L}(x)\leq 1{\text{ for all }}L\in {\mathcal {L}}\right\}}
    then p I ( x ) = sup { p L ( x ) : L ∈ L } {\displaystyle p_{I}(x)=\sup \left\{p_{L}(x):L\in {\mathcal {L}}\right\}} for all x ∈ X . {\displaystyle x\in X.}

The following examples show that the containment ( 0 , R ] K ⊆ ⋂ e > 0 ( 0 , R + e ) K {\displaystyle (0,R]K\;\subseteq \;{\textstyle \bigcap \limits _{e>0}}(0,R+e)K} could be proper.

Example: If R = 0 {\displaystyle R=0} and K = X {\displaystyle K=X} then ( 0 , R ] K = ( 0 , 0 ] X = ∅ X = ∅ {\displaystyle (0,R]K=(0,0]X=\varnothing X=\varnothing } but ⋂ e > 0 ( 0 , e ) K = ⋂ e > 0 X = X , {\displaystyle {\textstyle \bigcap \limits _{e>0}}(0,e)K={\textstyle \bigcap \limits _{e>0}}X=X,} which shows that its possible for ( 0 , R ] K {\displaystyle (0,R]K} to be a proper subset of ⋂ e > 0 ( 0 , R + e ) K {\displaystyle {\textstyle \bigcap \limits _{e>0}}(0,R+e)K} when R = 0. {\displaystyle R=0.} ◼ {\displaystyle \blacksquare }

The next example shows that the containment can be proper when R = 1 ; {\displaystyle R=1;} the example may be generalized to any real R > 0. {\displaystyle R>0.} Assuming that [ 0 , 1 ] K ⊆ K , {\displaystyle [0,1]K\subseteq K,} the following example is representative of how it happens that x ∈ X {\displaystyle x\in X} satisfies p K ( x ) = 1 {\displaystyle p_{K}(x)=1} but x ∉ ( 0 , 1 ] K . {\displaystyle x\not \in (0,1]K.}

Example: Let x ∈ X {\displaystyle x\in X} be non-zero and let K = [ 0 , 1 ) x {\displaystyle K=[0,1)x} so that [ 0 , 1 ] K = K {\displaystyle [0,1]K=K} and x ∉ K . {\displaystyle x\not \in K.} From x ∉ ( 0 , 1 ) K = K {\displaystyle x\not \in (0,1)K=K} it follows that p K ( x ) ≥ 1. {\displaystyle p_{K}(x)\geq 1.} That p K ( x ) ≤ 1 {\displaystyle p_{K}(x)\leq 1} follows from observing that for every e > 0 , {\displaystyle e>0,} ( 0 , 1 + e ) K = [ 0 , 1 + e ) ( [ 0 , 1 ) x ) = [ 0 , 1 + e ) x , {\displaystyle (0,1+e)K=[0,1+e)([0,1)x)=[0,1+e)x,} which contains x . {\displaystyle x.} Thus p K ( x ) = 1 {\displaystyle p_{K}(x)=1} and x ∈ ⋂ e > 0 ( 0 , 1 + e ) K . {\displaystyle x\in {\textstyle \bigcap \limits _{e>0}}(0,1+e)K.} However, ( 0 , 1 ] K = ( 0 , 1 ] ( [ 0 , 1 ) x ) = [ 0 , 1 ) x = K {\displaystyle (0,1]K=(0,1]([0,1)x)=[0,1)x=K} so that x ∉ ( 0 , 1 ] K , {\displaystyle x\not \in (0,1]K,} as desired. ◼ {\displaystyle \blacksquare }

Positive homogeneity characterizes Minkowski functionals

The next theorem shows that Minkowski functionals are exactly those functions f : X → [ 0 , ∞ ] {\displaystyle f:X\to [0,\infty ]} that have a certain purely algebraic property that is commonly encountered.

Theorem — Let f : X → [ 0 , ∞ ] {\displaystyle f:X\to [0,\infty ]} be any function. The following statements are equivalent:

  1. Strict positive homogeneity: f ( t x ) = t f ( x ) {\displaystyle \;f(tx)=tf(x)} for all x ∈ X {\displaystyle x\in X} and all positive real t > 0. {\displaystyle t>0.}
    • This statement is equivalent to: f ( t x ) ≤ t f ( x ) {\displaystyle f(tx)\leq tf(x)} for all x ∈ X {\displaystyle x\in X} and all positive real t > 0. {\displaystyle t>0.}
  2. f {\displaystyle f} is a Minkowski functional: meaning that there exists a subset S ⊆ X {\displaystyle S\subseteq X} such that f = p S . {\displaystyle f=p_{S}.}
  3. f = p K {\displaystyle f=p_{K}} where K := { x ∈ X : f ( x ) ≤ 1 } . {\displaystyle K:=\{x\in X:f(x)\leq 1\}.}
  4. f = p V {\displaystyle f=p_{V}\,} where V := { x ∈ X : f ( x ) < 1 } . {\displaystyle V\,:=\{x\in X:f(x)<1\}.}

Moreover, if f {\displaystyle f} never takes on the value ∞ {\displaystyle \,\infty \,} (so that the product 0 ⋅ f ( x ) {\displaystyle 0\cdot f(x)} is always well-defined) then this list may be extended to include:

  1. Positive/Nonnegative homogeneity: f ( t x ) = t f ( x ) {\displaystyle f(tx)=tf(x)} for all x ∈ X {\displaystyle x\in X} and all nonnegative real t ≥ 0. {\displaystyle t\geq 0.}
Proof

If f ( t x ) ≤ t f ( x ) {\displaystyle f(tx)\leq tf(x)} holds for all x ∈ X {\displaystyle x\in X} and real t > 0 {\displaystyle t>0} then t f ( x ) = t f ( 1 t ( t x ) ) ≤ t 1 t f ( t x ) = f ( t x ) ≤ t f ( x ) {\displaystyle tf(x)=tf\left({\tfrac {1}{t}}(tx)\right)\leq t{\tfrac {1}{t}}f(tx)=f(tx)\leq tf(x)} so that t f ( x ) = f ( t x ) . {\displaystyle tf(x)=f(tx).}

Only (1) implies (3) will be proven because afterwards, the rest of the theorem follows immediately from the basic properties of Minkowski functionals described earlier; properties that will henceforth be used without comment. So assume that f : X → [ 0 , ∞ ] {\displaystyle f:X\to [0,\infty ]} is a function such that f ( t x ) = t f ( x ) {\displaystyle f(tx)=tf(x)} for all x ∈ X {\displaystyle x\in X} and all real t > 0 {\displaystyle t>0} and let K := { y ∈ X : f ( y ) ≤ 1 } . {\displaystyle K:=\{y\in X:f(y)\leq 1\}.}

For all real t > 0 , {\displaystyle t>0,} f ( 0 ) = f ( t 0 ) = t f ( 0 ) {\displaystyle f(0)=f(t0)=tf(0)} so by taking t = 2 {\displaystyle t=2} for instance, it follows that either f ( 0 ) = 0 {\displaystyle f(0)=0} or f ( 0 ) = ∞ . {\displaystyle f(0)=\infty .} Let x ∈ X . {\displaystyle x\in X.} It remains to show that f ( x ) = p K ( x ) . {\displaystyle f(x)=p_{K}(x).}

It will now be shown that if f ( x ) = 0 {\displaystyle f(x)=0} or f ( x ) = ∞ {\displaystyle f(x)=\infty } then f ( x ) = p K ( x ) , {\displaystyle f(x)=p_{K}(x),} so that in particular, it will follow that f ( 0 ) = p K ( 0 ) . {\displaystyle f(0)=p_{K}(0).} So suppose that f ( x ) = 0 {\displaystyle f(x)=0} or f ( x ) = ∞ ; {\displaystyle f(x)=\infty ;} in either case f ( t x ) = t f ( x ) = f ( x ) {\displaystyle f(tx)=tf(x)=f(x)} for all real t > 0. {\displaystyle t>0.} Now if f ( x ) = 0 {\displaystyle f(x)=0} then this implies that that t x ∈ K {\displaystyle tx\in K} for all real t > 0 {\displaystyle t>0} (since f ( t x ) = 0 ≤ 1 {\displaystyle f(tx)=0\leq 1} ), which implies that p K ( x ) = 0 , {\displaystyle p_{K}(x)=0,} as desired. Similarly, if f ( x ) = ∞ {\displaystyle f(x)=\infty } then t x ∉ K {\displaystyle tx\not \in K} for all real t > 0 , {\displaystyle t>0,} which implies that p K ( x ) = ∞ , {\displaystyle p_{K}(x)=\infty ,} as desired. Thus, it will henceforth be assumed that R := f ( x ) {\displaystyle R:=f(x)} a positive real number and that x ≠ 0 {\displaystyle x\neq 0} (importantly, however, the possibility that p K ( x ) {\displaystyle p_{K}(x)} is 0 {\displaystyle 0} or ∞ {\displaystyle \,\infty \,} has not yet been ruled out).

Recall that just like f , {\displaystyle f,} the function p K {\displaystyle p_{K}} satisfies p K ( t x ) = t p K ( x ) {\displaystyle p_{K}(tx)=tp_{K}(x)} for all real t > 0. {\displaystyle t>0.} Since 0 < 1 R < ∞ , {\displaystyle 0<{\tfrac {1}{R}}<\infty ,} p K ( x ) = R = f ( x ) {\displaystyle p_{K}(x)=R=f(x)} if and only if p K ( 1 R x ) = 1 = f ( 1 R x ) {\displaystyle p_{K}\left({\tfrac {1}{R}}x\right)=1=f\left({\tfrac {1}{R}}x\right)} so assume without loss of generality that R = 1 {\displaystyle R=1} and it remains to show that p K ( 1 R x ) = 1. {\displaystyle p_{K}\left({\tfrac {1}{R}}x\right)=1.} Since f ( x ) = 1 , {\displaystyle f(x)=1,} x ∈ K ⊆ ( 0 , 1 ] K , {\displaystyle x\in K\subseteq (0,1]K,} which implies that p K ( x ) ≤ 1 {\displaystyle p_{K}(x)\leq 1} (so in particular, p K ( x ) ≠ ∞ {\displaystyle p_{K}(x)\neq \infty } is guaranteed). It remains to show that p K ( x ) ≥ 1 , {\displaystyle p_{K}(x)\geq 1,} which recall happens if and only if x ∉ ( 0 , 1 ) K . {\displaystyle x\not \in (0,1)K.} So assume for the sake of contradiction that x ∈ ( 0 , 1 ) K {\displaystyle x\in (0,1)K} and let 0 < r < 1 {\displaystyle 0<r<1} and k ∈ K {\displaystyle k\in K} be such that x = r k , {\displaystyle x=rk,} where note that k ∈ K {\displaystyle k\in K} implies that f ( k ) ≤ 1. {\displaystyle f(k)\leq 1.} Then 1 = f ( x ) = f ( r k ) = r f ( k ) ≤ r < 1. {\displaystyle 1=f(x)=f(rk)=rf(k)\leq r<1.} ◼ {\displaystyle \blacksquare }

This theorem can be extended to characterize certain classes of [ − ∞ , ∞ ] {\displaystyle [-\infty ,\infty ]} -valued maps (for example, real-valued sublinear functions) in terms of Minkowski functionals. For instance, it can be used to describe how every real homogeneous function f : X → R {\displaystyle f:X\to \mathbb {R} } (such as linear functionals) can be written in terms of a unique Minkowski functional having a certain property.

Characterizing Minkowski functionals on star sets

Proposition[10] — Let f : X → [ 0 , ∞ ] {\displaystyle f:X\to [0,\infty ]} be any function and K ⊆ X {\displaystyle K\subseteq X} be any subset. The following statements are equivalent:

  1. f {\displaystyle f} is (strictly) positive homogeneous, f ( 0 ) = 0 , {\displaystyle f(0)=0,} and
    { x ∈ X : f ( x ) < 1 } ⊆ K ⊆ { x ∈ X : f ( x ) ≤ 1 } . {\displaystyle \{x\in X:f(x)<1\}\;\subseteq \;K\;\subseteq \;\{x\in X:f(x)\leq 1\}.}
  2. f {\displaystyle f} is the Minkowski functional of K {\displaystyle K} (that is, f = p K {\displaystyle f=p_{K}} ), K {\displaystyle K} contains the origin, and K {\displaystyle K} is star-shaped at the origin.
    • The set K {\displaystyle K} is star-shaped at the origin if and only if t k ∈ K {\displaystyle tk\in K} whenever k ∈ K {\displaystyle k\in K} and 0 ≤ t ≤ 1. {\displaystyle 0\leq t\leq 1.} A set that is star-shaped at the origin is sometimes called a star set.[9]

Characterizing Minkowski functionals that are seminorms

In this next theorem, which follows immediately from the statements above, K {\displaystyle K} is not assumed to be absorbing in X {\displaystyle X} and instead, it is deduced that ( 0 , 1 ) K {\displaystyle (0,1)K} is absorbing when p K {\displaystyle p_{K}} is a seminorm. It is also not assumed that K {\displaystyle K} is balanced (which is a property that K {\displaystyle K} is often required to have); in its place is the weaker condition that ( 0 , 1 ) s K ⊆ ( 0 , 1 ) K {\displaystyle (0,1)sK\subseteq (0,1)K} for all scalars s {\displaystyle s} satisfying | s | = 1. {\displaystyle |s|=1.} The common requirement that K {\displaystyle K} be convex is also weakened to only requiring that ( 0 , 1 ) K {\displaystyle (0,1)K} be convex.

Theorem — Let K {\displaystyle K} be a subset of a real or complex vector space X . {\displaystyle X.} Then p K {\displaystyle p_{K}} is a seminorm on X {\displaystyle X} if and only if all of the following conditions hold:

  1. ( 0 , ∞ ) K = X {\displaystyle (0,\infty )K=X} (or equivalently, p K {\displaystyle p_{K}} is real-valued).
  2. ( 0 , 1 ) K {\displaystyle (0,1)K} is convex (or equivalently, p K {\displaystyle p_{K}} is subadditive).
    • It suffices (but is not necessary) for K {\displaystyle K} to be convex.
  3. ( 0 , 1 ) u K ⊆ ( 0 , 1 ) K {\displaystyle (0,1)uK\subseteq (0,1)K} for all unit scalars u . {\displaystyle u.}
    • This condition is satisfied if K {\displaystyle K} is balanced or more generally if u K ⊆ K {\displaystyle uK\subseteq K} for all unit scalars u . {\displaystyle u.}

in which case 0 ∈ K {\displaystyle 0\in K} and both ( 0 , 1 ) K = { x ∈ X : p ( x ) < 1 } {\displaystyle (0,1)K=\{x\in X:p(x)<1\}} and ⋂ e > 0 ( 0 , 1 + e ) K = { x ∈ X : p K ( x ) ≤ 1 } {\displaystyle \bigcap _{e>0}(0,1+e)K=\left\{x\in X:p_{K}(x)\leq 1\right\}} will be convex, balanced, and absorbing subsets of X . {\displaystyle X.}

Conversely, if f {\displaystyle f} is a seminorm on X {\displaystyle X} then the set V := { x ∈ X : f ( x ) < 1 } {\displaystyle V:=\{x\in X:f(x)<1\}} satisfies all three of the above conditions (and thus also the conclusions) and also f = p V ; {\displaystyle f=p_{V};} moreover, V {\displaystyle V} is necessarily convex, balanced, absorbing, and satisfies ( 0 , 1 ) V = V = [ 0 , 1 ] V . {\displaystyle (0,1)V=V=[0,1]V.}

Corollary — If K {\displaystyle K} is a convex, balanced, and absorbing subset of a real or complex vector space X , {\displaystyle X,} then p K {\displaystyle p_{K}} is a seminorm on X . {\displaystyle X.}

Positive sublinear functions and Minkowski functionals

It may be shown that a real-valued subadditive function f : X → R {\displaystyle f:X\to \mathbb {R} } on an arbitrary topological vector space X {\displaystyle X} is continuous at the origin if and only if it is uniformly continuous, where if in addition f {\displaystyle f} is nonnegative, then f {\displaystyle f} is continuous if and only if V := { x ∈ X : f ( x ) < 1 } {\displaystyle V:=\{x\in X:f(x)<1\}} is an open neighborhood in X . {\displaystyle X.} [11] If f : X → R {\displaystyle f:X\to \mathbb {R} } is subadditive and satisfies f ( 0 ) = 0 , {\displaystyle f(0)=0,} then f {\displaystyle f} is continuous if and only if its absolute value | f | : X → [ 0 , ∞ ) {\displaystyle |f|:X\to [0,\infty )} is continuous.

A nonnegative sublinear function is a nonnegative homogeneous function f : X → [ 0 , ∞ ) {\displaystyle f:X\to [0,\infty )} that satisfies the triangle inequality. It follows immediately from the results below that for such a function f , {\displaystyle f,} if V := { x ∈ X : f ( x ) < 1 } {\displaystyle V:=\{x\in X:f(x)<1\}} then f = p V . {\displaystyle f=p_{V}.} Given K ⊆ X , {\displaystyle K\subseteq X,} the Minkowski functional p K {\displaystyle p_{K}} is a sublinear function if and only if it is real-valued and subadditive, which is happens if and only if ( 0 , ∞ ) K = X {\displaystyle (0,\infty )K=X} and ( 0 , 1 ) K {\displaystyle (0,1)K} is convex.

Correspondence between open convex sets and positive continuous sublinear functions

Theorem[11] — Suppose that X {\displaystyle X} is a topological vector space (not necessarily locally convex or Hausdorff) over the real or complex numbers. Then the non-empty open convex subsets of X {\displaystyle X} are exactly those sets that are of the form z + { x ∈ X : p ( x ) < 1 } = { x ∈ X : p ( x − z ) < 1 } {\displaystyle z+\{x\in X:p(x)<1\}=\{x\in X:p(x-z)<1\}} for some z ∈ X {\displaystyle z\in X} and some positive continuous sublinear function p {\displaystyle p} on X . {\displaystyle X.}

Proof

Let V ≠ ∅ {\displaystyle V\neq \varnothing } be an open convex subset of X . {\displaystyle X.} If 0 ∈ V {\displaystyle 0\in V} then let z := 0 {\displaystyle z:=0} and otherwise let z ∈ V {\displaystyle z\in V} be arbitrary. Let p = p K : X → [ 0 , ∞ ) {\displaystyle p=p_{K}:X\to [0,\infty )} be the Minkowski functional of K := V − z {\displaystyle K:=V-z} where this convex open neighborhood of the origin satisfies ( 0 , 1 ) K = K . {\displaystyle (0,1)K=K.} Then p {\displaystyle p} is a continuous sublinear function on X {\displaystyle X} since V − z {\displaystyle V-z} is convex, absorbing, and open (however, p {\displaystyle p} is not necessarily a seminorm since it is not necessarily absolutely homogeneous). From the properties of Minkowski functionals, we have p K − 1 ( [ 0 , 1 ) ) = ( 0 , 1 ) K , {\displaystyle p_{K}^{-1}([0,1))=(0,1)K,} from which it follows that V − z = { x ∈ X : p ( x ) < 1 } {\displaystyle V-z=\{x\in X:p(x)<1\}} and so V = z + { x ∈ X : p ( x ) < 1 } . {\displaystyle V=z+\{x\in X:p(x)<1\}.} Since z + { x ∈ X : p ( x ) < 1 } = { x ∈ X : p ( x − z ) < 1 } , {\displaystyle z+\{x\in X:p(x)<1\}=\{x\in X:p(x-z)<1\},} this completes the proof. ◼ {\displaystyle \blacksquare }

See also

Notes

  1. ^ It is in general false that x ∈ r D {\displaystyle x\in rD} if and only if p D ( x ) = r {\displaystyle p_{D}(x)=r} (for example, consider when p K {\displaystyle p_{K}} is a norm or a seminorm). The correct statement is: If 0 < r < ∞ {\displaystyle 0<r<\infty } then x ∈ r D {\displaystyle x\in rD} if and only if p D ( x ) = r {\displaystyle p_{D}(x)=r} or p D ( x ) = 0. {\displaystyle p_{D}(x)=0.}
  2. ^ u {\displaystyle u} is having unit length means that | u | = 1. {\displaystyle |u|=1.}
  3. ^ The map p K {\displaystyle p_{K}} is called absolutely homogeneous if | s | p K ( x ) {\displaystyle |s|p_{K}(x)} is well-defined and p K ( s x ) = | s | p K ( x ) {\displaystyle p_{K}(sx)=|s|p_{K}(x)} for all x ∈ X {\displaystyle x\in X} and all scalars s {\displaystyle s} (not just non-zero scalars).

References

  1. ^ Narici & Beckenstein 2011, p. 109.
  2. ^ Narici & Beckenstein 2011, p. 119.
  3. ^ a b Jarchow 1981, pp. 104–108.
  4. ^ a b Narici & Beckenstein 2011, pp. 115–154.
  5. ^ a b Schaefer 1999, p. 40.
  6. ^ a b c Narici & Beckenstein 2011, p. 119-120.
  7. ^ Kubrusly 2011, p. 200.
  8. ^ a b Schechter 1996, p. 316.
  9. ^ Schechter 1996, p. 303.
  10. ^ Schechter 1996, pp. 313–317.
  11. ^ a b Narici & Beckenstein 2011, pp. 192–193.
  • Berberian, Sterling K. (1974). Lectures in Functional Analysis and Operator Theory. Graduate Texts in Mathematics. Vol. 15. New York: Springer. ISBN 978-0-387-90081-0. OCLC 878109401.
  • Bourbaki, Nicolas (1987) [1981]. Topological Vector Spaces: Chapters 1–5. Éléments de mathématique. Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag. ISBN 3-540-13627-4. OCLC 17499190.
  • Conway, John (1990). A course in functional analysis. Graduate Texts in Mathematics. Vol. 96 (2nd ed.). New York: Springer-Verlag. ISBN 978-0-387-97245-9. OCLC 21195908.
  • Diestel, Joe (2008). The Metric Theory of Tensor Products: Grothendieck's Résumé Revisited. Vol. 16. Providence, R.I.: American Mathematical Society. ISBN 9781470424831. OCLC 185095773.
  • Dineen, Seán (1981). Complex Analysis in Locally Convex Spaces. North-Holland Mathematics Studies. Vol. 57. Amsterdam New York New York: North-Holland Pub. Co., Elsevier Science Pub. Co. ISBN 978-0-08-087168-4. OCLC 16549589.
  • Dunford, Nelson; Schwartz, Jacob T. (1988). Linear Operators. Pure and applied mathematics. Vol. 1. New York: Wiley-Interscience. ISBN 978-0-471-60848-6. OCLC 18412261.
  • Edwards, Robert E. (1995). Functional Analysis: Theory and Applications. New York: Dover Publications. ISBN 978-0-486-68143-6. OCLC 30593138.
  • Grothendieck, Alexander (1973). Topological Vector Spaces. Translated by Chaljub, Orlando. New York: Gordon and Breach Science Publishers. ISBN 978-0-677-30020-7. OCLC 886098.
  • Hogbe-Nlend, Henri (1977). Bornologies and Functional Analysis: Introductory Course on the Theory of Duality Topology-Bornology and its use in Functional Analysis. North-Holland Mathematics Studies. Vol. 26. Amsterdam New York New York: North Holland. ISBN 978-0-08-087137-0. MR 0500064. OCLC 316549583.
  • Hogbe-Nlend, Henri; Moscatelli, V. B. (1981). Nuclear and Conuclear Spaces: Introductory Course on Nuclear and Conuclear Spaces in the Light of the Duality "topology-bornology". North-Holland Mathematics Studies. Vol. 52. Amsterdam New York New York: North Holland. ISBN 978-0-08-087163-9. OCLC 316564345.
  • Husain, Taqdir; Khaleelulla, S. M. (1978). Barrelledness in Topological and Ordered Vector Spaces. Lecture Notes in Mathematics. Vol. 692. Berlin, New York, Heidelberg: Springer-Verlag. ISBN 978-3-540-09096-0. OCLC 4493665.
  • Keller, Hans (1974). Differential Calculus in Locally Convex Spaces. Lecture Notes in Mathematics. Vol. 417. Berlin New York: Springer-Verlag. ISBN 978-3-540-06962-1. OCLC 1103033.
  • Khaleelulla, S. M. (1982). Counterexamples in Topological Vector Spaces. Lecture Notes in Mathematics. Vol. 936. Berlin, Heidelberg, New York: Springer-Verlag. ISBN 978-3-540-11565-6. OCLC 8588370.
  • Kubrusly, Carlos S. (2011). The Elements of Operator Theory (Second ed.). Boston: Birkhäuser. ISBN 978-0-8176-4998-2. OCLC 710154895.
  • Jarchow, Hans (1981). Locally convex spaces. Stuttgart: B.G. Teubner. ISBN 978-3-519-02224-4. OCLC 8210342.
  • Köthe, Gottfried (1983) [1969]. Topological Vector Spaces I. Grundlehren der mathematischen Wissenschaften. Vol. 159. Translated by Garling, D.J.H. New York: Springer Science & Business Media. ISBN 978-3-642-64988-2. MR 0248498. OCLC 840293704.
  • Köthe, Gottfried (1979). Topological Vector Spaces II. Grundlehren der mathematischen Wissenschaften. Vol. 237. New York: Springer Science & Business Media. ISBN 978-0-387-90400-9. OCLC 180577972.
  • Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
  • Pietsch, Albrecht (1979). Nuclear Locally Convex Spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete. Vol. 66 (Second ed.). Berlin, New York: Springer-Verlag. ISBN 978-0-387-05644-9. OCLC 539541.
  • Robertson, Alex P.; Robertson, Wendy J. (1980). Topological Vector Spaces. Cambridge Tracts in Mathematics. Vol. 53. Cambridge England: Cambridge University Press. ISBN 978-0-521-29882-7. OCLC 589250.
  • Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
  • Thompson, Anthony C. (1996). Minkowski Geometry. Encyclopedia of Mathematics and Its Applications. Cambridge University Press. ISBN 0-521-40472-X.
  • Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
  • Schechter, Eric (1996). Handbook of Analysis and Its Foundations. San Diego, CA: Academic Press. ISBN 978-0-12-622760-4. OCLC 175294365.
  • Schaefer, H. H. (1999). Topological Vector Spaces. New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
  • Swartz, Charles (1992). An introduction to Functional Analysis. New York: M. Dekker. ISBN 978-0-8247-8643-4. OCLC 24909067.
  • Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
  • Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
  • Wong, Yau-Chuen (1979). Schwartz Spaces, Nuclear Spaces, and Tensor Products. Lecture Notes in Mathematics. Vol. 726. Berlin New York: Springer-Verlag. ISBN 978-3-540-09513-2. OCLC 5126158.

Further reading

  • F. Simeski, A.M.P. Boelens and M. Ihme. Modeling Adsorption in Silica Pores via Minkowski Functionals and Molecular Electrostatic Moments. Energies 13 (22) 5976 (2020). https://doi.org/10.3390/en13225976
  • v
  • t
  • e
Spaces
Properties
TheoremsOperatorsAlgebrasOpen problemsApplicationsAdvanced topics
  • Category
  • v
  • t
  • e
Basic concepts
Main results
Maps
Types of sets
Set operations
Types of TVSs
  • Category
  • v
  • t
  • e
Basic concepts
Topics (list)
Maps
Main results (list)
Sets
Series
Duality
Applications and related